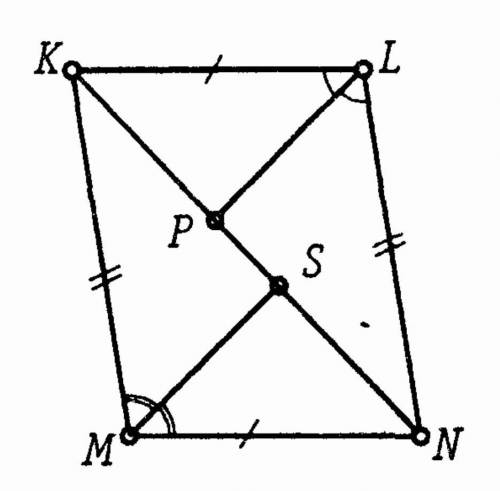
Здесь нужно найти СУС или УСУ Умоляю вас.​

Добрый день!

Для решения данной задачи нам потребуется использовать теорему о внешнем касательном угле.

В заданном изображении, линия, которая проходит через точку G, перпендикулярна к отрезку АС. Отсюда мы можем заключить, что угол GAC является прямым углом, так как перпендикуляр и основание образуют прямой угол.

Согласно теореме, угол GAC должен быть равен углу SCD, где S - точка касания окружности (в данном случае это точка F), C - центр окружности, а D - точка, которая лежит на окружности.

Таким образом, мы можем сделать вывод, что угол GAC равен углу SCD.

Обратите внимание, что у нас также есть угол GFC, у которого неизвестное значение. Мы можем рассмотреть его значение, используя свойства треугольника.

В треугольнике GFC, сумма всех углов равна 180 градусов. Мы уже знаем, что угол GAC равен 90 градусам, и угол SCD равен углу GAC. Если мы обозначим угол GFC как x, то получим следующее уравнение:

90 + x + угол GFC = 180.

Для решения уравнения, найдем значение угла GFC:

x + угол GFC = 180 - 90,

x + угол GFC = 90.

Теперь у нас есть два уравнения:

угол GFC = 90 - x (1)

угол GFC = угол SFD (2).

Так как угол GFC и угол SFD представляют собой один и тот же угол, мы можем приравнять уравнения (1) и (2):

90 - x = угол SFD.

Теперь у нас есть значение угла GFC равное 90 - x, а также равенство угла GFC и угла SFD.

Следовательно, угол SFD также равен 90 - x.

Таким образом, мы можем ответить на вопрос: СУС или УСУ равно 90 - x.