Задания контрольной работы №1 по дисциплине "Техническое черчение"
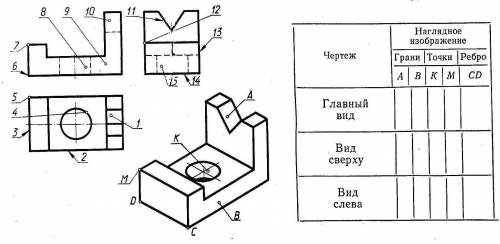
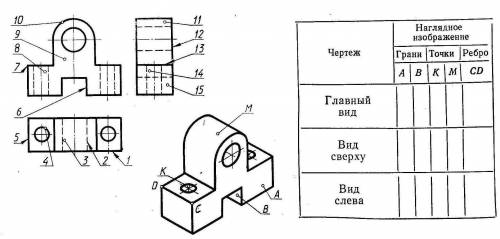
Другие вопросы по теме Геометрия
Популярные вопросы
- Даны координаты двух точек на плоскости. Если хотя бы одна из них лежит на какой-нибудь...
3 - Як поставилася Мирослава до союзу її батька з монголами?...
3 - гелiкоптер пролетiв 180 км зi швидкiстю 50м/с. Скiльки обертiв здiйснить за час...
1 - Различия грибов и бактерий...
1 - 38° пн. ш. 14° сх.д. какого места координати?...
1 - с контрольной по географии...
2 - Точка Е лижить між точками К і Р і ділить відрізок КР = 42СМ на відрізки довжини...
1 - Метод телекоммуникаций что это?...
1 - Халык тағылымындағы айға карап колыны шошайтпа» аген тыйым салари16.мағынасыПр,...
2 - 1. Функция спроса D =7-p , функция предложенияS=-2+2р. -Определить равновесную...
1
На чертеже изображен треугольник ABC. Сначала определим его вид по углам и сторонам. Обратим внимание на соотношение сторон и знаки углов:
AB = AC, ∠A = 90°, ∠C = 45°, ∠B = 45°.
Так как угол A равен 90°, треугольник ABC является прямоугольным. Далее, так как у всех углов треугольника ABC одинаковая величина (45°), то мы также можем назвать его равнобедренным.
Задание 2:
На чертеже представлен прямоугольник ABCD. Для начала, определим длины всех сторон прямоугольника:
AB = 6 см, BC = 3 см, CD = 6 см, DA = 3 см.
Пункт а) Требуется найти периметр прямоугольника. Периметр - это сумма длин всех сторон прямоугольника. Для данного прямоугольника находится по формуле: P = AB + BC + CD + DA = 6 + 3 + 6 + 3 = 18 см.
Пункт б) Найдем площадь прямоугольника. Площадь прямоугольника находится по формуле: S = AB * BC = 6 * 3 = 18 см².
Пункт в) Определим диагонали прямоугольника. По теореме Пифагора, диагональ - это гипотенуза прямоугольного треугольника, в котором катеты равны сторонам прямоугольника. Найдем длину диагоналей:
AC = √(AB² + BC²) = √(6² + 3²) = √(36 + 9) = √45 = 6.71 см.
BD = √(BC² + CD²) = √(3² + 6²) = √(9 + 36) = √45 = 6.71 см.
Задание 3:
На чертеже изображен треугольник AFG. Сначала определим его вид по углам и сторонам. Обратим внимание на соотношение сторон и знаки углов:
AF = AG, ∠A = 90°, ∠G = 30°, ∠F = 60°.
Так как угол A равен 90°, треугольник AFG является прямоугольным. Далее, так как углы G и F равны 30° и 60° соответственно, то мы также можем назвать этот треугольник двугранным или прямоугольным с углами 30° и 60°.
Задание 4:
На чертеже изображен параллелограмм ABCD.
Сначала, определим параллельность противоположных сторон:
AB || CD (параллельность обозначается двумя параллельными линиями).
Пункт а) Найдем периметр параллелограмма. Периметр - это сумма длин всех сторон параллелограмма. Для данного параллелограмма находим по формуле: P = AB + BC + CD + DA = 6 + 7 + 6 + 7 = 26 см.
Пункт б) Найдем площадь параллелограмма. Площадь параллелограмма равна произведению длины одной из сторон на высоту, опущенную на эту сторону. Высота - это перпендикуляр, опущенный из вершины параллелограмма на его сторону.
Для нахождения площади параллелограмма необходимо найти высоту. Для этого можно воспользоваться формулой площади прямоугольника, где S = AB * h, где h - высота.
Используя формулу площади, получим S = AB * h. Так как высота не задана, проведем ее из вершины A к стороне BC. Параметр h перпендикулярен стороне AB и равен расстоянию между этой стороной и стороной CD. Перпендикулярные стороны AB и CD, поэтому границы перпендикуляра являются границами соответствующих отрезков (длины AB и CD равны). Теперь находим значение h, используя формулу площади прямоугольника: S = AB * h = 6 см * 4 см = 24 см².
Таким образом, площадь параллелограмма равна 24 см².