Задание и рисунок на карточках

Объяснение:

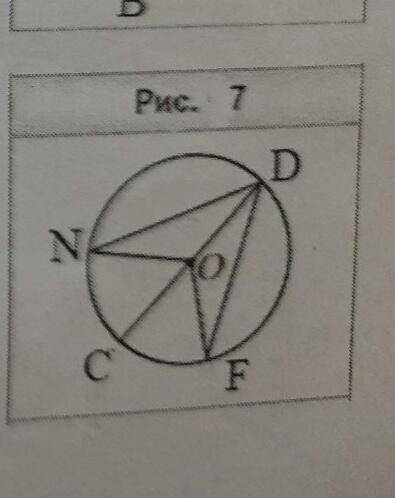
Рассмотрим треугольники ∆NOD и ∆FOD

<NOD=<FOD, по условию.

DO- общая сторона.

NO=OF=R, радиусы.

∆NOD=∆FOF, по первому признаку.

В равных треугольниках соответственные стороны равны.

DN=DF, что и требовалось доказать.

∠NOD=∠FOD (из условия)

ON, OD, OF - радиусы окружности, значит ON=OD=OF

По признаку СУС (ON=OF, ∠NOD=∠FOD, OD - смежная сторона) ΔNOD=ΔFOD) ΔDON=ΔDOF

Если треугольники равны, то и стороны треугольников соответственно равны, значит DN=DF