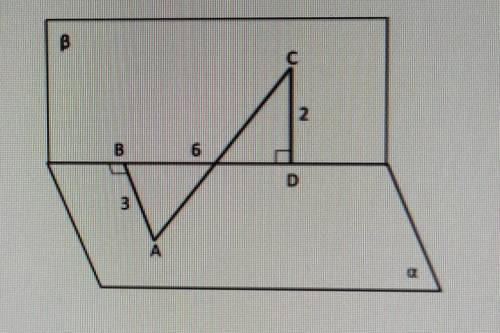
Задание 8 Вопрос: Плоскости аир перпендикулярны. АВ
перпендикулярно BD, CD перпендикулярно BD,
AB = 3, BD = 6, CD = 2. Найдите длину AC.​

Для того чтобы решить данную задачу, мы можем использовать теорему Пифагора.

1. В начале давайте построим геометрическую модель задачи. Мы имеем две плоскости AIR и ABD, причем AB является перпендикуляром к BD, и плоскость CD также перпендикулярна BD.

2. Теперь, посмотрите на треугольник ABD. У нас есть две известные стороны - AB и BD. Мы можем использовать теорему Пифагора, чтобы найти третью сторону AD. Так как AB = 3 и BD = 6, мы можем записать уравнение:

AB^2 + BD^2 = AD^2

3^2 + 6^2 = AD^2

9 + 36 = AD^2

45 = AD^2

4. Теперь найдем AD, взяв квадратный корень обеих сторон уравнения:

AD = √45

AD = √(9 * 5)

AD = 3√5

5. Посмотрим на треугольник ACD. Мы знаем, что CD = 2 и AD = 3√5. Нас просят найти длину AC.

6. Мы можем снова использовать теорему Пифагора для треугольника ACD. Записываем уравнение:

AC^2 = AD^2 + CD^2

AC^2 = (3√5)^2 + 2^2

AC^2 = 9 * 5 + 4

AC^2 = 45 + 4

AC^2 = 49

7. Чтобы найти длину AC, снова возьмем квадратный корень обеих сторон уравнения:

AC = √49

AC = 7

Таким образом, длина AC равна 7.