Задание 4 ( ).

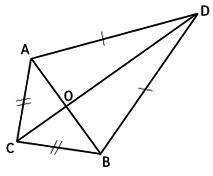
Точки А и В расположены по разные стороны от прямой CD так, что AC = CB, AD = BD. Докажите, что AO = OB, где О – точка пересечения отрезков AB и СD.

Добрый день! Рассмотрим данную задачу.

У нас есть прямая CD и точки A и B, которые расположены по разные стороны от этой прямой. Также известно, что AC равно CB и AD равно BD. Наша задача - доказать, что точка O, которая является точкой пересечения отрезков AB и CD, делит отрезок AB пополам, то есть, что AO равно OB.

Начнем с построения дополнительных отрезков и проведения вспомогательных линий. Обозначим точки пересечения отрезков AC и BD как точку E. Также проведем через точку O прямую EF параллельную прямой CD. Получившиеся конструкции показаны ниже:

[вставить изображение с построенными отрезками и линиями]

Теперь мы можем применить теорему Талеса для треугольников AOF и BOE. Согласно теореме Талеса, если точка G делит отрезок AB в отношении AG : BG = AO : BO, то прямые CG и DF параллельны.

Чтобы это доказать, нам нужно узнать отношение AG к BG. Заметим, что треугольники ADC и BDC равнобедренные (по условию AC = CB и AD = BD). Поэтому углы ACD и BCD равны. Также углы ACB и AD между самими собой равны. Поэтому треугольники ACD и BCD равны по двум углам и общей стороне CD. Следовательно, у них равны также и гипотенузы AO и BO.

Теперь возьмем во внимание треугольники AOF и BOE. У нас есть два равных угла ACD и BCD. Также, так как CD || EF, то углы ACB и EFD равны (как соответственные углы). Поэтому по теореме угловой суммы углов треугольники AOF и BOE имеют суммарную меру 180 градусов и являются подобными по теореме АА (по двум углам). Таким образом, они имеют одинаковые отношения для соответствующих сторон. Известно, что AO равно AE, и мы хотим узнать отношение AG к BG, поэтому сосредоточимся на треугольниках AOF и BOE.

Так как треугольники AOF и BOE подобны, то отношение AG к BG равно AO к BO. Но мы знаем, что AO равно AE, так как AC = CB. Получается, что AG = BG. Это означает, что отрезок AB делится точкой O пополам. То есть, AO равно OB.

Таким образом, мы доказали, что если точки A и B находятся по разные стороны от прямой CD, и при этом AC равно CB и AD равно BD, то точка O, являющаяся точкой пересечения отрезков AB и CD, делит отрезок AB пополам, то есть, AO равно OB.