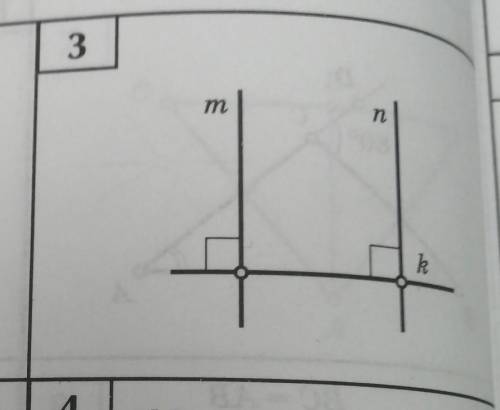
Задание 3. Учебник по геометрии 7-9 класс Э. Н. Балаян. Признаки параллельности прямых
Другие вопросы по теме Геометрия
Популярные вопросы
- 1. какая масса воды разложилась при действии электрического тока,...
2 - Напишите стихи лермонтова михаила юрьевича...
3 - Посредством суффиксов и пристаков образуйте производные слова с корнями...
3 - Вследующих сочетаниях слов замените выделенные слова другими словами,...
3 - 25 . краткое описание покровского и кистеневки! не сравнение их усадьб!...
1 - Put the verbs in brackets into the present continuous passive. 6....
3 - Слово с наибольшим количеством однокореных слов...
2 - 1) из скольких клеток построено тело губок? 2) есть ли у губок клетки...
2 - Сделать небольшой рассказ на тему марнае чаканне тэкли...
3 - Найти объём (v) кислорода если количество молекул его равно n=3*10^32...
3
а можно условие
1. Первый признак: параллельные прямые имеют одинаковый угол наклона (наклонные параллельные прямые).
Данный признак можно использовать, когда прямые заданы уравнениями вида y = kx + b, где k – коэффициент наклона.
Например, прямые, заданные уравнениями y = 2x + 3 и y = 2x - 1, имеют одинаковый коэффициент наклона 2, следовательно, они параллельны.
2. Второй признак: параллельные прямые имеют пропорциональные углы наклона.
Данный признак применим, когда прямые заданы в виде уравнений в общем виде Ax + By + C = 0.
Например, прямые, заданные уравнениями 2x + 3y - 1 = 0 и 4x + 6y - 2 = 0, имеют пропорциональные коэффициенты, соответственно, 2/3 и 4/6, следовательно, они параллельны.
3. Третий признак: параллельные прямые расположены относительно одной прямой.
Данный признак заключается в том, что если две прямые параллельны третьей прямой, то они будут параллельны друг другу.
Например, на рисунке даны две прямые a и b, которые параллельны прямой CD:
A_____________________ B + --- \
\
\ \
\ \
\
C_____D
Таким образом, из рисунка видно, что прямые a и b параллельны, так как они лежат вне прямой CD и не пересекают ее.
4. Четвертый признак: параллельные прямые имеют равные нормальные векторы.
Нормальным вектором прямой называется вектор, перпендикулярный данной прямой.
Если две прямые параллельны, то их нормальные векторы равны.
Например, если нормальные векторы прямых A и B имеют компоненты (1, 0) и (1, 0) соответственно, то прямые A и B параллельны.
В данном задании необходимо определить, какие из указанных пар прямых являются параллельными. Найдите на рисунке параллельные прямые и обведите их номера.