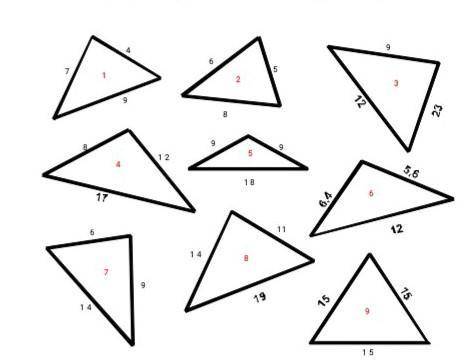
Задание 2 Какие треугольники не существуют?
​

Для определения, какие треугольники не существуют, мы должны использовать два правила: неравенство треугольника и сумму внутренних углов треугольника.

1. Неравенство треугольника:
Согласно этому правилу, сумма длин любых двух сторон треугольника должна быть больше, чем длина третьей стороны. Если это неравенство нарушается для любой пары сторон, то треугольник не может существовать.

2. Сумма внутренних углов треугольника:
Сумма всех внутренних углов треугольника всегда равна 180 градусам. Если сумма углов не равна 180 градусам, то такой треугольник не может существовать.

Теперь посмотрим на заданную фигуру.


У нас есть три разные комбинации сторон, которые мы должны проверить:

1. Стрелка А:
a = 5, b = 10, c = 8
Проверяем неравенство треугольника:
a + b > c
5 + 10 > 8
15 > 8 (Верно)

a + c > b
5 + 8 > 10
13 > 10 (Верно)

b + c > a
10 + 8 > 5
18 > 5 (Верно)

Проверяем сумму углов:
Угол 1 + Угол 2 + Угол 3 = 92 + 36 + 52 = 180 (Верно)

Вывод: Треугольник со сторонами 5, 10 и 8 существует.

2. Стрелка B:
a = 7, b = 3, c = 6
Проверяем неравенство треугольника:
a + b > c
7 + 3 > 6
10 > 6 (Верно)

a + c > b
7 + 6 > 3
13 > 3 (Верно)

b + c > a
3 + 6 > 7
9 < 7 (Неверно)

Вывод: Такой треугольник не может существовать, так как нарушается неравенство треугольника.

3. Стрелка C:
a = 4, b = 4, c = 9
Проверяем неравенство треугольника:
a + b > c
4 + 4 > 9
8 < 9 (Неверно)

Вывод: Треугольник со сторонами 4, 4 и 9 не может существовать, так как нарушается неравенство треугольника.

Таким образом, изображенный на рисунке треугольник может существовать только со сторонами 5, 10 и 8. Треугольники со сторонами 7, 3 и 6, а также 4, 4 и 9 не могут существовать.