Задание 1. Написать уравнение прямой, проходящей через точку (1,2) и перпендикулярную вектору (3,-5). Задание 2. Объясните, как вычислить расстояние между скрещивающимися прямыми, если известны их параметрические уравнения.
Задание 3. Объясните, как найти расстояние от точки (1, 2, 3) до прямой
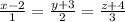
Другие вопросы по теме Геометрия
Популярные вопросы
- Прочитай имена существительные. Выпиши в один столбик имена существительные...
3 - Прочитай текст. Какова его главная мысль? Какое изменение произошло...
2 - Свободный диктант. Прочитай. • Почему автору кажется, что ёжик...
2 - Продолжи запись. Запиши как можно больше имён существительных,...
1 - ответь на вопрос и запиши слова-ответы. Как называется человек,...
1 - Образуй от основ данных существительных с суффиксов -их-, -иц-,...
3 - Образуй как можно больше имён существительных от основ данных слов...
2 - Придумай и запиши маленькую сказку о героях, которые живут в волшебной...
2 - В своей речи мы часто употребляем сокращённые имена, когда общаемся....
1 - Площадь трёх комнатной квартиры равна 80 кв. м. Вс помещения составляют...
2
Задание 1. Написать уравнение прямой, проходящей через точку (1,2) и перпендикулярную вектору (3,-5).
Координаты перпендикулярного вектора (3,-5) - это коэффициенты общего уравнения прямой: 3х - 5у + С = 0.
Подставим координаты точки .через которую проходит прямая.
3*1 - 5*2 + С = 0.
С = 10 - 3 = 7.
ответ: уравнение 3х - 5у + 7 = 0.
Задание 2. Объясните, как вычислить расстояние между скрещивающимися прямыми, если известны их параметрические уравнения.
Оно равно смешанному произведение векторов, делённому на
векторное произведение векторов.
Задание 3. Объясните, как найти расстояние от точки (1, 2, 3) до прямой
(x-2)/1 = (y+3)/2 = (z+4)/3.
Из свойств векторного произведения известно, что модуль векторного произведения векторов равен площади параллелограмма построенного на этих векторах.
s = 1; 2; 3 - направляющий вектор прямой;
M1 = 2; -3; -4 - точка лежащая на прямой.
Тогда M0M1 = {M1x - M0x; M1y - M0y; M1z - M0z} =
(2 - 1; -3 - 2; -4 - 3) = (1; -5; -7).
Площадь параллелограмма лежащего на двух векторах M0M1 и s:
S = |M0M1 × s|
M0M1 × s =
i j k
1 -5 -7
1 2 3 =
= i(-5·3 - (-7)·2) - j(1·3 - (-7)·1) + k (1·2 - (-5)·1) =
= i(-15 + 14) - j(3 + 7) + k(2 + 5) = (-1; -10; 7).
Зная площадь параллелограмма и длину стороны, найдем высоту (расстояние от точки до прямой):
d = |M0M1×s|
|s|
= √((-1)² + (-10)² + 7²)
√(1² + 2² + 3²)
= √150
√14
= √(75 /7)
= 5√21
7
≈ 3.273268.