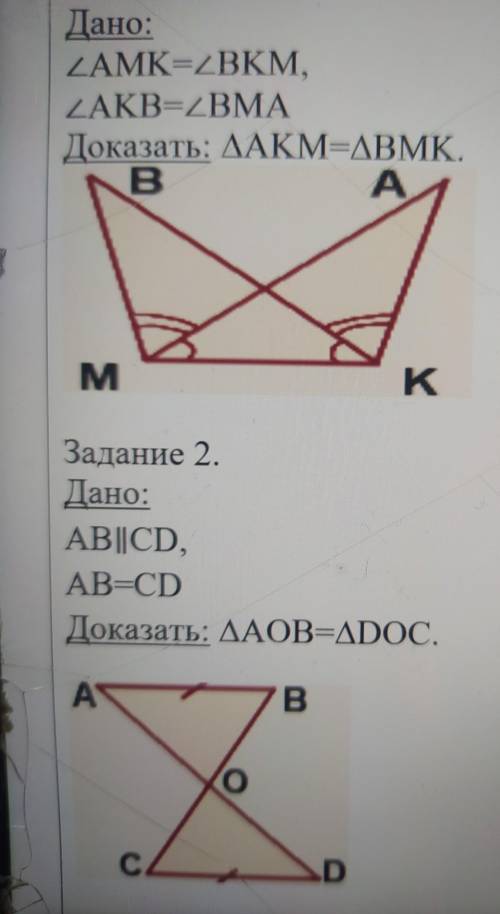
Задание 1.

Дано:

∠AMK=∠BKM,

∠AKB=∠BMA

Доказать: ∆AKM=∆BMK.

Задание 2.

Дано:

AB∥CD,

AB=CD

Доказать: ∆AOB=∆DOC.​

Задание 1:

Дано: ∠AMK = ∠BKM, ∠AKB = ∠BMA

Доказываем: ∆AKM = ∆BMK

Для начала, построим отрезки AM и BM.

По условию, у нас есть равенство углов ∠AMK = ∠BKM. Это означает, что мы можем сказать, что угол AKM = BKM.

Также по условию задачи ∠AKB = ∠BMA. Это значит, что угол AKB = BMA.

Теперь мы можем сделать вывод, что треугольники ∆AKM и ∆BMK могут быть подобны, так как у них равны углы AKM и BKM (по свойству подобных треугольников – углы внутри треугольника равны, если соответствующие им углы равны).

Также мы знаем, что соответствующие стороны подобных треугольников пропорциональны. Поэтому мы можем сказать, что отношение стороны AM к стороне BM равно отношению стороны AK к стороне BK.

Теперь рассмотрим следующий факт: у нас есть равенство углов AKB = BMA, а также отношение сторон AM/BM = AK/BK. Это означает, что треугольники ∆AKB и ∆BMA равны по теореме сходных треугольников.

Исходя из равенства треугольников ∆AKB и ∆BMA, следует, что ∆AKM = ∆BMK (равныосторонние треугольники).

Задание 2:

Дано: AB || CD, AB = CD

Доказываем: ∆AOB = ∆DOC

По условию задачи, мы имеем параллельные прямые AB и CD. Это означает, что угол AOB и угол DOC являются поперечными углами и равны друг другу.

Также, по условию AB = CD, и у нас имеются две стороны – AO и BO.

Мы также знаем, что в треугольнике ∆AOB и ∆DOC углы AOB и DOC равны, так как они являются поперечными углами при параллельных прямых.

Теперь рассмотрим стороны треугольников ∆AOB и ∆DOC. По условию задачи, AB = CD, что означает, что сторона AO и сторона OC равны, так как они являются противоположными сторонами прямоугольников AB и CD.

Таким образом, у нас есть равные соответствующие углы и равные соответствующие стороны, поэтому мы можем сказать, что ∆AOB = ∆DOC по теореме о одинаковых треугольниках.

В обоих заданиях мы использовали свойства подобных треугольников, теорему о равенстве треугольников и свойства параллельных прямых. Используя данные свойства и углы, мы доказали равенство треугольников.