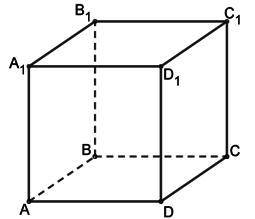
Задан куб (см. рис.). а) Изобразите 3 некомпланарных вектора, начала и концы которых лежат в вершинах этого куба.
б) Выразите вектор DN через эти 3 вектора. Точка N – середина ребра ВВ1.
Запишите полное решение со всеми необходимыми пояснениями.
Другие вопросы по теме Геометрия
Популярные вопросы
- Все по картине сделайте последние ...
2 - Сравни экосистемы по плану видовой состав и вид энергии...
1 - 2. На координатной плоскости отмечены точки: A(-3- 2) , B(6; 4), C(-2; 0), D(-7;...
1 - Моток дроту розрізали на три частини.довдина регої частини 48м. Довжина другої становила...
3 - Антоніми до слів: Рідкісний Подібність Недоречний Стосовно (що стосується)...
2 - Какие две скульптуры получили своё развитие в бронзовом веке в Центральной Азии...
3 - 320:80*810:90 порядок действий...
1 - Спрогнозируйте, что может ожидать человечество в будущем, если отношение к окружающей...
1 - Жұмыс сөзінен екі түбірлес сөз жаса...
2 - 5. Образуй из прилагательных существительные и наоборот sauber – zuverlässig – ordentlich...
2
Выберем вершины А, B и C куба, которые не лежат на одной грани.
Пусть A(x₁, y₁, z₁), B(x₂, y₂, z₂) и C(x₃, y₃, z₃) - координаты выбранных вершин.
Тогда, чтобы найти вектор, соединяющий начало и конец вектора, мы можем использовать следующую формулу:
Вектор AB = (x₂ - x₁, y₂ - y₁, z₂ - z₁)
Вектор AC = (x₃ - x₁, y₃ - y₁, z₃ - z₁)
Примерно таким образом мы можем найти 3 некомпланарных вектора, начала и концы которых лежат в вершинах куба.
б) Теперь давайте рассмотрим вектор DN. Мы знаем, что точка N является серединой ребра ВВ1.
Поскольку B(x₂, y₂, z₂) и B1(x₂, y₂, 0) являются вершинами ребра ВВ1, то координаты точки N будут равны:
Nx = (x₂ + x₂)/2 = x₂
Ny = (y₂ + y₂)/2 = y₂
Nz = (z₂ + 0)/2 = z₂/2
Таким образом, координаты точки N равны (x₂, y₂, z₂/2).
Для того чтобы выразить вектор DN через три вектора AB, AC и BC (начала и концы которых лежат в вершинах куба), мы можем применить формулу скалярного произведения:
Вектор DN = Вектор AN - Вектор AD
Выразим каждый из этих векторов через векторы AB, AC и BC:
Вектор AN = Вектор AB + Вектор BN
Вектор AD = Вектор AB + Вектор BD
Теперь вставим эти выражения в формулу вектора DN:
Вектор DN = (Вектор AB + Вектор BN) - (Вектор AB + Вектор BD)
Заметим, что вектор AB сокращается:
Вектор DN = Вектор BN - Вектор BD
Таким образом, вектор DN равен разности вектора BN и вектора BD.
Надеюсь, это решение ясно объяснило как найти 3 некомпланарных вектора, начала и концы которых лежат в вершинах куба, и как выразить вектор DN через эти 3 вектора. Если у вас возникнут еще вопросы, пожалуйста, не стесняйтесь спрашивать!