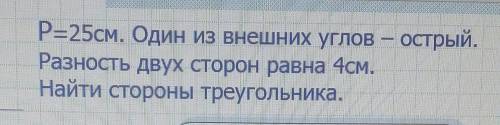
Задачка, p=25, один из внешних углов-острый. Разность двух сторон ровная 4 см. Найти стороны треугольника
Другие вопросы по теме Геометрия
Популярные вопросы
- Можно будет решить в 6 составь выражение если и значение ученик потерял по действиям...
2 - Прилетела жар-птица, села на яблоню и начала щипать золотые яблоки. Где в этом...
1 - Машина приехала по прямой дороге 6 км затем...
3 - Si Упражнение 1. sho Переведите на английский язык (Используйте Present, Past,...
1 - Напишите рассказ от лица барских детей из рассказа кукушка...
3 - Роль в формировании Казахского ханства Жанибек хан...
1 - ОТ ГЛАГОЛОВ ОБРАЗУЙТЕ ВСЕ ВОЗМОЖНЫЕ ФОРМЫ ДЕЕПРИЧАСТИЙ...
2 - Синквейн герои Великой Отечественной войны...
2 - Можете написать любой стихотворение о Великой Отечественной войне (не обязательно...
2 - Изменился бы смысл стихотворение Если бы оно называлось Смерть Пушкина? ответ:...
1
Дано, что один из внешних углов треугольника является острым. Это означает, что сумма двух других углов должна быть меньше 180 градусов. В треугольнике сумма всех углов равна 180 градусов.
Для начала, найдем меру внешнего угла. Известно, что сумма углов в треугольнике равна 180 градусов. Значит, внутренние углы треугольника образуют сумму в 180 - (180 - 90) = 90 градусов. Так как один из внешних углов является острым, его мера будет 180 - 90 = 90 градусов.
Далее, нам известна разность двух сторон треугольника, которая равна 4 см. Пусть x - это меньшая сторона треугольника, а y - это большая сторона треугольника. Тогда можно составить следующую систему уравнений, используя известные данные:
x + y = 25 - формула для периметра (p=25).
y - x = 4 - формула для разности сторон.
Решим эту систему уравнений методом сложения или вычитания. Для этого сложим или вычтем оба уравнения.
(x + y) + (y - x) = 25 + 4
2y = 29
y = 29/2
y = 14.5
Теперь, используя найденное значение y, найдем значение x:
y - x = 4
14.5 - x = 4
x = 14.5 - 4
x = 10.5
Итак, меньшая сторона треугольника равна 10.5 см, а большая сторона равна 14.5 см.
Ответ: стороны треугольника равны 10.5 см и 14.5 см.