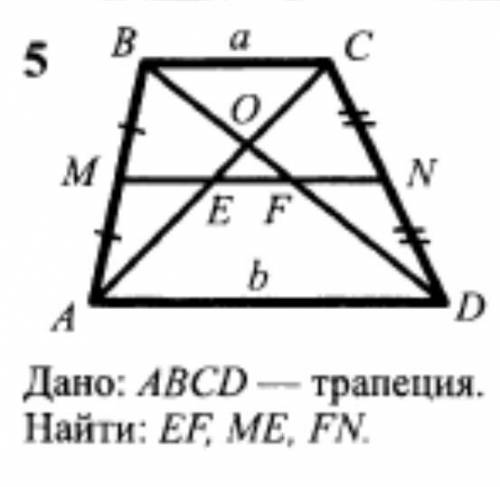
Задача по геометрии

прописать хотя бы кратко процесс решения

Здравствуй!

Данная задача из геометрии связана с нахождением площади трехугольника. Для её решения необходимо применить формулу площади треугольника, которая гласит:

Площадь треугольника = (основание × высота) ÷ 2.

Процесс решения данной задачи можно разбить на следующие шаги:

Шаг 1: Определение основания и высоты треугольника.

На изображении данного треугольника, основание — это отрезок BC, а высота проведена от вершины A, перпендикулярно к основанию BC.

Шаг 2: Измерение длины основания и высоты.

Узнать длину основания BC и высоты, проведенной из вершины A, помогут предоставленные нам значения. На рисунке видно, что высота (AH) равна 4 см.

Для нахождения длины основания BC, можно воспользоваться теоремой Пифагора в прямоугольном треугольнике ABC. Для этого, необходимо воспользоваться формулой:

a² + b² = c²,

где a и b — катеты треугольника, c — гипотенуза.

В нашем случае, гипотенуза AC — это отрезок AB, длина которого равна 10 см, а катеты являются отрезками BC и AC, обозначенными на рисунке. Получаем уравнение:

(BC)² + (4)² = (10)².

Подставляем известные значения:

(BC)² + 16 = 100.

При переносе значения 16 на другую сторону уравнения, получаем:

(BC)² = 100 - 16,

(BC)² = 84.

Шаг 3: Нахождение длины основания BC.

Для того чтобы найти значение BC, извлекаем квадратный корень с обеих сторон уравнения, получаем:

BC = √84.

Длина основания BC равна корню из 84. Дальнейшие вычисления требуют использования калькулятора или таблицы квадратных корней.

Шаг 4: Подсчет площади треугольника.

Теперь, когда у нас есть измерения основания BC и высоты AH, мы можем найти площадь треугольника, используя формулу:

Площадь треугольника = (основание × высота) ÷ 2,

Подставляем значения:

Площадь треугольника = (BC × AH) ÷ 2.

Площадь треугольника = (√84 × 4) ÷ 2.

Вычисляем значение под корнем:

Площадь треугольника = (2√21 × 4) ÷ 2.

Упрощаем выражение:

Площадь треугольника = 2√21.

Таким образом, площадь данного треугольника равна 2√21 квадратных сантиметров.

Это краткий процесс решения данной задачи по геометрии. Если возникнут какие-либо дополнительные вопросы, не стесняйся задавать!