Задача по геометрии 7 класс
Другие вопросы по теме Геометрия
Популярные вопросы
- Серединний перпендикуляр гіпотенузи AB прямокутного трикутника ABC...
1 - Складіть рівняння реакцій , за до яких можна здійснити перетворення...
1 - Скоротіть дріб (√15-√5)/√5...
1 - Указать, в каком предложении встречается деепричастный оборот (знаки...
1 - Які країни взяли участь у колоніальному поділі Африки?...
1 - В результате снижения цен на отдельные товары величина ВВП в планируемом...
2 - К отделу мохообразные принадлежит: а)фукус б) политрих обыкновенный...
3 - - Мышленности. Приенной специализации являются сельское хозяйство...
3 - мне с полным объяснением (чем вы руководстовались, когда выбирали...
2 - На прикладах творів Індійського культурного регіону поясніть, як...
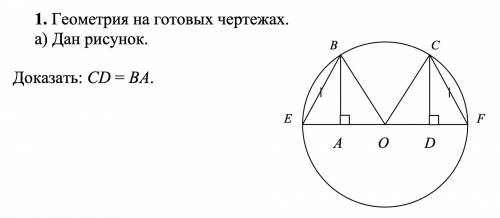
2
Объяснение:
∠ВЕО=∠СФЕ ,вписанные углы опирающиеся на одинаковые дуги.
дуга ВС- общая ,дуга ЕВ= дуге СФ (дуги ,стянутые равными хордами) Значит сумма равных величин равныВС+ЕВ=ВС+СФ,а значит и вписанные углы,опирающиеся на эти дуги равны
УВ=СФ (дано) ЕО=ДФ (радиусы)
по двум сторонам и углу между ними Δ ЕВО ≅ ΔФСО
∠ВАЕ=∠СДФ=90°
ЕВ=СФ,∠ВЕА= ∠СФВ (из доказательства выше,против равных сторон) Значит ΔВЕА≅ΔСФД по 4 признаку( по стороне,прилежащему углу и углу против большей стороны) Значит ВА=СД ,против равных углов.
Треугольники с указанными высотами ОЕ и ОF? являются равнобедренными и равными по 3 признаку равенства треугольников, в них ОВ=ОЕ=ОF=OС равны как радиусы одной окружности, а ВЕ=FС равны по условию. значит, СD=ВА, как высоты, проведенные к соответственно равным сторонам ОЕ и ОF.