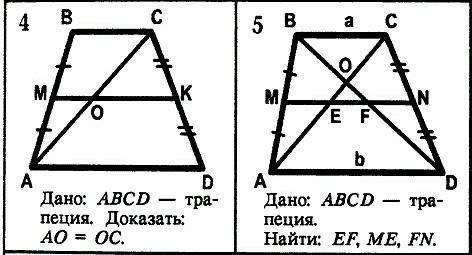
Задача: N°#1 Дано: ABCD-трапеция
Доказать: АО=ОС
Задача: N°#2
Дано: АВСD-трапеция
Найти: ЕF, ME, FN
Другие вопросы по теме Геометрия
Популярные вопросы
- Обьем прямоугольного параллелепипеда 25.2 дм.длина основания 3.5...
2 - Какие города основадижаыбек и керей . надо...
3 - Периметр равнобедренного треугольника равен 13 см, а основание...
3 - Камень массой 800г падает не землю с высоты 4 м. какую работу...
2 - Число групп сцепления прямо пропарциаонально числу...
1 - Вычисли площадь квадрата с длиной стороны 80 дм...
1 - Почему несмотря на относительно небольшие масштабы выигранных...
1 - Составьте рассказ про окружающую среду её загрязнение и что люди...
2 - За 1,8 огурцов и 2,4 кг. помидоров заплатили 2,16тыс. рублей....
1 - ответить на вопрос прием предложений вот и хитрый одуванчик не...
2
Дано: ABCD - трапеция
Доказать: АО = ОС
Решение:
1. Изобразим данную трапецию:
A ------- B
| |
| |
| |
D ------- C
2. Обозначим точку пересечения диагоналей трапеции ABCD как точку O.
A ------- B
| |
| O |
| |
D ------- C
3. В трапеции ABCD сторона AB параллельна стороне CD, поэтому углы ACD и ABD являются соответственными углами.
4. Вспомним свойства соответственных углов: если две пары углов одной фигуры соответственно равны, то эти фигуры подобны.
5. Так как трапеция ABCD - подобная фигура, то соответствующие отрезки на этих фигурах будут пропорциональны.
6. В данном случае, мы знаем, что AO - это диагональ трапеции ABCD, а OC - это одна из боковых сторон трапеции.
7. Следовательно, AO и OC должны быть пропорциональны друг другу.
8. Так как в трапеции минимальная диагональ делит максимальную диагональ на две равные части, то можно сделать вывод, что АО = ОС.
Таким образом, АО = ОС.
Задача №2:
Дано: АВСD - трапеция
Найти: ЕF, ME, FN
Решение:
1. Изобразим данную трапецию:
A ------- B
| |
| E |
| |
D ------- C
2. Заметим, что точка Е - это середина основания АС трапеции, а точка F - середина основания BD трапеции.
3. Таким образом, отрезок ЕF будет перпендикулярен и параллелен основаниям трапеции ABCD.
4. Для нахождения длины ЕF можно воспользоваться теоремой Пифагора, так как треугольник ЕDF является прямоугольным.
ED^2 + DF^2 = EF^2
5. Зная, что длина основания АС равна 8 см, а длина основания BD равна 14 см, мы можем найти длину ED и DF, так как они равны половине длин оснований соответственно:
ED = AC / 2 = 8 / 2 = 4 см
DF = BD / 2 = 14 / 2 = 7 см
6. Подставляем полученные значения в формулу Пифагора:
EF^2 = ED^2 + DF^2 = 4^2 + 7^2 = 16 + 49 = 65
7. Извлекаем квадратный корень из обеих частей уравнения:
EF = √65
Таким образом, получаем, что длина EF равна √65 см.
8. Для нахождения длин ME и FN можно воспользоваться подобными треугольниками.
9. Заметим, что треугольники AEF и MEF подобны (так как угол E общий, а угол AFE и угол MEF - прямые углы). Значит, отношение соответствующих сторон этих треугольников будет одинаково.
AE / MF = EF / ME
10. Нам известны длины AE (= AC / 2 = 8 / 2 = 4 см) и EF (= √65 см), поэтому можем записать соотношение:
4 / MF = √65 / ME
11. Аналогично, треугольники DEF и FNE подобны, поэтому:
DE / FN = EF / NE
12. Заметим, что DE = ED (= 4 см), EF = √65 см, поэтому можем записать соотношение:
4 / FN = √65 / NE
13. Из уравнений (10) и (12) выразим MF и FN через ME и NE:
MF = 4 * ME / √65
FN = 4 * NE / √65
Таким образом, мы нашли выражения для длин MF и FN через длины ME и NE.