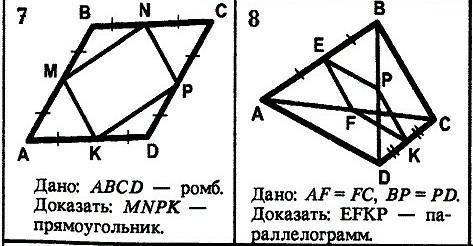
Задача: N°#1 Дано: ABCD-ромб
Доказать: MNPK-прямоугольник

Задача: N°#2

Дано: AF=FC, BP=PD
Доказать: EFKP-паралеллограм​

Задача №1: Доказать, что MNPK - прямоугольник, если дано, что ABCD – ромб.

Для начала вспомним свойства ромба. Ромб – это четырехугольник, у которого все стороны равны. Также известно, что диагонали ромба перпендикулярны и делят его на четыре равных треугольника.

Рассмотрим ромб ABCD. Пусть M – точка пересечения диагоналей AC и BD. Для доказательства того, что MNPK – прямоугольник, нам нужно показать, что у него все углы равны 90 градусов.

Возьмем треугольник MDC. Так как диагонали ромба перпендикулярны и делят его на равные треугольники, то угол MDC будет равен 90 градусов.

Теперь рассмотрим треугольник MAC. Так же, как и в предыдущем случае, угол MAC будет равен 90 градусов.

Итак, мы доказали, что углы MDC и MAC в треугольниках MDC и MAC равны 90 градусов. Это значит, что углы NMP и NKP в прямоугольнике MNPK также равны 90 градусов. Значит, прямоугольник MNPK доказан.

Задача №2: Доказать, что EFKP – параллелограмм, если дано, что AF = FC и BP = PD.

Для доказательства того, что EFKP – параллелограмм, нам нужно показать, что противоположные стороны параллельны и равны.

Из условия задачи имеем, что AF = FC и BP = PD. Таким образом, отрезки AF и FC равны по длине, и отрезки BP и PD также равны.

Рассмотрим треугольник AFE. У нас дано, что AF = FC, и угол AFE является внутренним углом треугольника. В треугольнике, у которого две стороны равны, а угол между ними является внутренним углом, противоположная сторона будет параллельна этим сторонам. Таким образом, сторона EF будет параллельна стороне AC.

Аналогично, рассмотрим треугольник BPD. У нас дано, что BP = PD, и угол BPD является внутренним углом треугольника. Таким образом, сторона PD будет параллельна стороне BC.

Из полученных результатов видно, что сторона EF параллельна стороне AC и сторона PD параллельна стороне BC. Значит, EFKP является параллелограммом.

Таким образом, мы доказали, что MNPK – прямоугольник и EFKP – параллелограмм, исходя из данных условий задачи.