Задача 3.
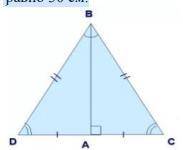
В равнобедренном треугольнике проведена медиана к основанию. Угол
напротив основания равен 60° . Найдите боковую сторону, если основание
равно 30 см.

Для решения данной задачи, нам понадобится использовать свойство медианы в равнобедренном треугольнике.

В равнобедренном треугольнике медиана, проведенная к основанию, также является биссектрисой и высотой этого треугольника.

Угол напротив основания равнобедренного треугольника равен 60 градусов.

Так как медиана является высотой, то у нее перпендикулярно основанию будет образован прямоугольный треугольник.

К сожалению, на изображении задачи не видно вершины треугольника, но предположим, что медиана полностью лежит внутри треугольника и пересекает основание на равном расстоянии от его середины.

Обозначим боковую сторону треугольника как "a". Для нахождения ее значения, воспользуемся теоремой Пифагора для прямоугольного треугольника, образованного медианой, половиной основания и боковой стороной треугольника.

Согласно теореме Пифагора, сумма квадратов катетов равна квадрату гипотенузы:

\(c^2 = a^2 + b^2\)

Где "c" - гипотенуза, "a" и "b" - катеты.

В нашей задаче, медиана будет выступать в роли гипотенузы, половина основания - в роли одного катета, а боковая сторона - в роли второго катета.

Так как угол напротив основания равен 60 градусов, а треугольник равнобедренный, то у нас получается равнобедренный прямоугольный треугольник.

Таким образом, у нас будет следующая система уравнений:

\(a^2 + \left(\dfrac{30}{2}\right)^2 = c^2\)

\(a^2 + 15^2 = c^2\)

\(a^2 + 225 = c^2\)

\(a^2 = c^2 - 225\)

Теперь, чтобы найти значение боковой стороны "а", нам нужно найти значение гипотенузы "c". Выполним это, применяя теорему косинусов:

Мы знаем, что у нас равнобедренный треугольник, поэтому мы можем использовать свойство равенства боковых сторон треугольника для нахождения угла α у основания треугольника:

\(α + α + 60 = 180\) (сумма углов треугольника равна 180°)

\(2α + 60 = 180\)

\(2α = 180 - 60\)

\(2α = 120\)

\(α = 60°\)

Теперь, используя теорему косинусов, мы можем найти значение гипотенузы "с":

\(c^2 = a^2 + b^2 - 2ab \cdot \cos α\)

\(c^2 = a^2 + 15^2 - 2a \cdot 15 \cdot \cos 60\)

\(c^2 = a^2 + 225 - 30a \cdot \dfrac{1}{2}\)

\(c^2 = a^2 + 225 - 15a\)

\(c^2 = a^2 - 15a + 225\)

Теперь мы можем заменить \(c^2\) в нашем уравнении для \(a^2\):

\(a^2 = a^2 + 225 - 15a\)

\(0 = 225 - 15a\)

\(15a = 225\)

\(a = \dfrac{225}{15}\)

\(a = 15\)

Таким образом, боковая сторона треугольника равна 15 см.