Задача 2. Доказать: Δ АВС=Δ АДС Задача 3. Доказать: Δ АВД=Δ ВСД
Задача 7. Доказать: АВ=АС

Обязательно с Дано, Найти, Решение к каждой задаче

Дано: В треугольнике АВС проведены медианы АД и ВС, и точка D - их точка пересечения.

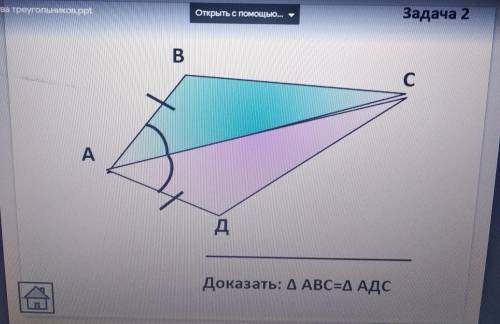
Найти: Доказать, что треугольники АВС и АДС равны между собой (Δ АВС = Δ АДС).

Решение:
Для доказательства равенства треугольников АВС и АДС возьмем во внимание теорему о равенстве треугольников по двум сторонам и углу между ними (SSS - сторона-сторона-сторона).

1. Проверим, являются ли стороны треугольников АВС и АДС равными:

Дано, что АВ - медиана, следовательно, АВ = ВС (так как медиана делит сторону пополам).
Дано также, что АD - медиана, значит, AD = AS.
Таким образом, АВ = AS.

2. Проверим, равны ли углы треугольников АВС и АДС:

Из данного изображения видно, что углы ВАС и САD равны (так как это вертикальные углы), а углы АВС и АДС равны (так как это углы, вписанные в полуокружность).

Теперь у нас есть два равных угла и одна равная сторона, что соответствует теореме SSS о равенстве треугольников. Следовательно, треугольник АВС равен треугольнику АДС, что и требовалось доказать (Δ АВС = Δ АДС).

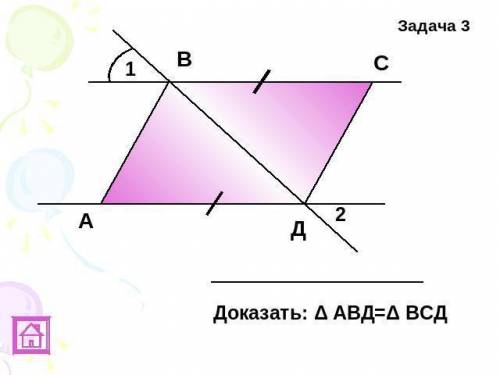
Задача 3. Доказать: Δ АВД=Δ ВСД

Дано: В треугольнике АВС проведены медианы АД и ВС, и точка D - их точка пересечения.

Найти: Доказать, что треугольники АВД и ВСД равны между собой (Δ АВД = Δ ВСД).

Решение:
Аналогично предыдущему решению, воспользуемся теоремой SSS о равенстве треугольников.

1. Проверим, равны ли стороны треугольников АВД и ВСД:

Дано, что АВ - медиана и ВС - также медиана, следовательно, АВ = ВС (так как медиана делит сторону пополам).
Таким образом, АВ = ВС.

2. Проверим, равны ли углы треугольников АВД и ВСД:

Из данного изображения видно, что углы АВД и ВСД равны (так как это углы, вписанные в полуокружность) и углы ВАД и СДВ равны (так как это вертикальные углы).

Теперь у нас есть два равных угла и одна равная сторона, что соответствует теореме SSS о равенстве треугольников. Следовательно, треугольник АВД равен треугольнику ВСД, что и требовалось доказать (Δ АВД = Δ ВСД).

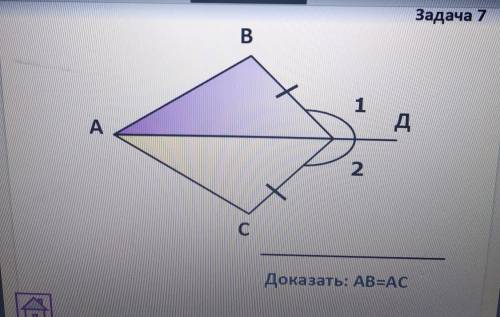
Задача 7. Доказать: АВ = АС

Дано: В треугольнике АВС проведены медианы АД и ВС, и точка D - их точка пересечения.

Найти: Доказать, что сторона АВ равна стороне АС (АВ = АС).

Решение:

1. Из предыдущего решения мы уже знаем, что сторона АВ равна стороне ВС, так как обе являются медианами треугольника АВС.

2. Из теоремы о треугольниках, проведенных медианами, следует, что точка их пересечения D делит каждую медиану в отношении 2:1.

Таким образом, можно сказать, что АВ и АС являются частями одной и той же медианы АД. Поскольку они являются равными частями этой медианы, можно заключить, что АВ = АС, что и требовалось доказать.