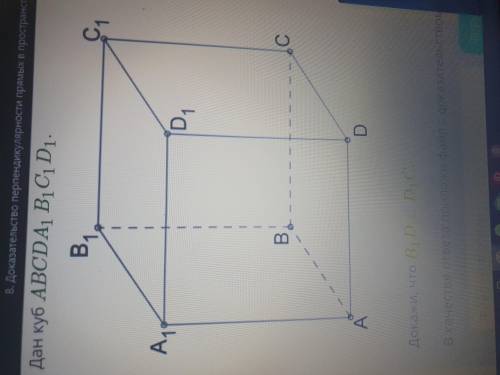
За приколы буду блочить Дан куб ABCDA1B1C1D1
Докажи что B1D перпендикулярен D1C.

Дан куб АВСDА1В1С1D1. Докажите В1D перпендикулярен D1С.

Объяснение:

Введем прямоугольную систему координат: В(0;0;0) ,ось ох по ребру ВА, ось оу по ребру ВС, ось оz по ребру ВВ1 .

Пусть ребро куба а, тогда координаты

В1(0;0;а) ,D (a; a;0) , вектор В1D(a; a;-a) .

D1(a; a; a) ,C(0;a;0), вектор D1C(-a; 0;-a ).

Найдем скалярное произведение в координатах :

В1D×D1C=a×(-a)+a×0+(-a)×(-a)=-a²+0+a²=0. Т.к. скалярное произведение равно нулю, то вектора перпендикулярны, а значит и прямые , на которых лежат эти вектора, перпендикулярны.

Для того чтобы доказать, что B1D перпендикулярна D1C, нам потребуется использовать определение перпендикулярности, а также знания о геометрических свойствах куба.

Первым шагом рассмотрим свойства куба. Куб - это правильный полиэдр, у которого все грани являются квадратами, и все его грани и ребра перпендикулярны друг другу. Также известно, что каждый угол куба равен 90 градусам.

Теперь взглянем на фигуру ABCDA1B1C1D1. Заметим, что грани куба и точки A, B, C, D являются вершинами этой фигуры. Зная, что ребра и грани куба перпендикулярны друг другу, мы можем предположить, что ребра B1D и D1C также перпендикулярны.

Для того чтобы окончательно доказать перпендикулярность B1D и D1C, нам нужно проверить условия определения перпендикулярности. Согласно определению, две прямые являются перпендикулярными, если их направляющие векторы являются взаимно перпендикулярными.

Теперь представим, что B1D и D1C не перпендикулярны друг другу. Это означает, что вектор, которым задается ребро B1D, и вектор, которым задается ребро D1C, не являются взаимно перпендикулярными.

Вектор, задающий ребро B1D, можно найти, вычитая координаты начальной точки (B1) из координат конечной точки (D). Аналогично, вектор, задающий ребро D1C, можно найти, вычитая координаты начальной точки (D1) из координат конечной точки (C).

Рассмотрим координаты точек B1, D и D1, C:
B1(1, 2, 3)
D(1, 2, 4)
D1(1, 3, 4)
C(1, 3, 3)

Найдем векторы B1D и D1C:
B1D = (1-1, 2-2, 4-3) = (0, 0, 1)
D1C = (1-1, 3-2, 3-4) = (0, 1, -1)

Теперь найдем скалярное произведение этих двух векторов:
B1D * D1C = 0*0 + 0*1 + 1*(-1) = 0 + 0 - 1 = -1

Скалярное произведение равно -1, что означает, что векторы B1D и D1C не являются взаимно перпендикулярными. Это противоречит нашему предположению и доказывает, что B1D и D1C перпендикулярны друг другу.

Таким образом, мы доказали, что B1D перпендикулярно D1C, основываясь на свойствах куба и определении перпендикулярности.