З точки до прямої проведено дві похилі .Одна з них довжиною 24 см утворює з прямою кут 45°. Знайдіть довжину другої похилої , якщо її проекція на пряму дорівнює 18 см
Другие вопросы по теме Геометрия
Популярные вопросы
- Переведи на язык: ❤️ я не буду вас ждать когда я занята....
2 - Много ! напишите уравнения реакций, при которых можно осуществить следующие...
3 - Алюминиевая проводка мамой 2,7 кг имеет поперечное сечение в форме квадрата...
1 - При межмолекулярной дегидратации алканола образуется 7,4 г простого эфира,а...
2 - Вальбоме 1105 марок,число иностранных морок составляли 30% от числа советских...
3 - Какое предложение осложнено обращением? выберите вариант ответа: друзья мои,...
3 - Сочинение по про отпуск 60-80 предложений...
2 - План описания положения материка. австралия. 1. положение относительно условных...
2 - Сколько существуеи различных прямоугольников площади которых 45см²...
3 - Решить уравнение: 5x+1/8=1/3. /-это дробь...
3
2√153 см ≈ 24,74 см
Объяснение:
1) 24 - це довжина гіпотенузи; а тому кут, який вона утворює з прямою дорівнює 45°, то обидва катета (один з них - довжина проекції, а інший-висота, відстань від точки до прямої) рівні. Приймемо довжину катета за х.
Тоді, згідно з теоремою Піфагора:
х² + х² = 24²
2х²=576
х² = 288
х = √288 см
2) Довжину другої похилої L знаходимо також за теоремою Піфагора:
L = √(18² + (√288)²) = √(324 + 288) = √612 = 2√153 ≈ 24,74 см
Відповідь: 2√153 см ≈ 24,74 см
1) 24 - это длина гипотенузы, а т.к. угол, который она образует с прямой равен 45°, то оба катета (один из них - длина проекции, а другой - высота, расстояние от точки до прямой) равны. Примем длину катета за х.
Тогда, согласно теореме Пифагора:
х² + х² = 24²
2х²=576
х² = 288
х = √288 см
2) Длину второй наклонной L находим также по теореме Пифагора:
L = √(18² + (√288)²) = √(324 + 288) = √612 = 2√153 ≈ 24,74 см
Довжина другої похилої 24.7 cм
Объяснение:
Відстань від точки до прямої дорівнює
h=24*sin45°=12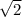 cм
cм
Довжина другої похилої дорівнює
в=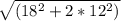 =24.7 cм
=24.7 cм