Xерез вершину d1 и середину ребра ad куба abcda1b1c1d1 проведена плоскость, параллельная прямой ac. вычислите периметр сечения, если ребро куба равно 16см
Astr4lis
3
22.05.2019 02:50
2
Другие вопросы по теме Геометрия
slovendim
03.05.2019 16:44
KrisChuHD
03.05.2019 16:53
Dimon200315
03.05.2019 16:54
DENTEX
03.05.2019 16:56
graincop
03.05.2019 17:03
ReichMan
25.04.2020 12:59
Angelina922
25.04.2020 12:59
cherrpaha
25.04.2020 12:59
MimINL
05.04.2021 12:08
Популярные вопросы
- Запиши текст под диктовку. озаглавь его. ранним утром я возвращался...
3 - Вставьте пропущенные буквы и знаки препинания в текст в (не)больш..й...
2 - Какие знания об окружающем мире важно для рыбаков какие для гончаров?...
3 - Составить план стиха леса -чудеса 2 класс...
2 - Слово парнишка какую имеет стилистическую окраску? (книжная или разговорная)...
2 - Дайте краткую содержание .об арионе...
1 - Вратарь – это последний бастион в спортивной игре. (2)когда противники...
3 - Мама пропалывает огород за 12 часов а дочка за 24 часа за какое время...
2 - Какую массу серы сожнли, если в результате выделилось 67,2 л оксда серы...
2 - Стилистическая окраска слова бросились. подберите синоним к этому слову...
3
Найдем КТ:![\sqrt[8]{2}](/tpl/images/0170/0450/97def.png)
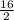= 8
![\sqrt[8]{5}](/tpl/images/0170/0450/1ec7c.png)
КТ = √(KD2+TD2)
КТ = √(64+64) =
КТ =
Значит,
KD = TD =
Получаем:
D1K = D1T =
√(KD2+D1D2) =
√(64+256) =
P =![\sqrt[16]{5}](/tpl/images/0170/0450/13bc6.png)
+ ![\sqrt[8]{2}](/tpl/images/0170/0450/97def.png)
= 8 * ( ![\sqrt[2]{5}](/tpl/images/0170/0450/ec2fb.png)
+ √2 )