1. Геометрия
  2. What is the sum of the meausures

What is the sum of the meausures of the interior angles of a polygon which has 20 diagonals

Fire73 Fire73    3   02.09.2021 14:18    0

Ответы
GenaTurboKrytt GenaTurboKrytt  02.09.2021 14:20

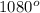ответ: 1080^o.

Объяснение:

If the number of diagonals is 20, then the number of corners is:

N=\dfrac{n(n-3)}{2} N \: - \: \text {number of diagonals};\\n \: - \: \text {number of angles}.\\

N=2020=\dfrac{n(n-3)}{2} n(n-3)=2 \cdot 20n^{2} -3n=40n^{2} -3n-40=0D=(-3)^{2} -4 \cdot (-40)=9+160=169=13^{2} n =\dfrac{3+13}{2} =8

Formula to find the sum of interior angles of a n-sided polygon:

S_{n} =(n-2) \cdot 180^oS_{n} =(8-2) \cdot 180^o=6 \cdot 180^o=1080^o

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
marinka10k marinka10k  26.07.2019 04:11
Найдите площадь прямоугольного треугольника если гипотенуза 20 см а сумма катетов 28 см...
1993nnnn 1993nnnn  26.07.2019 04:11
Найдите радиус окружности, вписаной в треугольник со сторонами 10, 24, 26...
masha12566 masha12566  16.08.2019 14:00
Углы,вписанные в окружноссть опирается на хорду ав,которая делитокружность в отношении 3: 5 .найдите величину вписвнных углов...
nabludatel00 nabludatel00  18.05.2020 23:07
Найти тангенс угла альфа прямоугольного, если катет в=6 см, а гипотенуза с=10см​...
zgonnikovakisa11 zgonnikovakisa11  18.05.2020 23:06
В равнобокой трапеции боковая сторона равна 8 см, средняя линия – 12 см. Найдите периметр трапеции....
Krooop04 Krooop04  18.05.2020 23:06
На высоте CD, опущенной из вершины С прямоугольноготреугольника АВС на гипотенузу AB, как на диаметре построенаокружность, которая пересекает катет АС в точке Е, а катет ВС​...
pamagiteplease pamagiteplease  23.06.2019 06:00
Основанием прямой треугольной призмы является прямоугольник с катетами 5 и2 боковое ребро призмы равно 12см . найдите объём призмы ....
ThePud ThePud  23.06.2019 06:00
Вравнобедренном треугольнике авс основание равно 12 см,а высота проведённая к нему 8 см. найти синус, косинус, тангенс углов при основании...
dany20skribka dany20skribka  23.06.2019 06:00
Катеты прямоугольного треугольника равны √15 и 1.найдите синус наименьшего угла этого треугольника....
julia071201 julia071201  23.06.2019 06:00
1.найдите радиус окружности, описанной около прямоугольника, две стороны которого равны 27 и корень из 295 2.найдите диагональ прямоугольника вписанного в окружность радиус которой...

Популярные вопросы