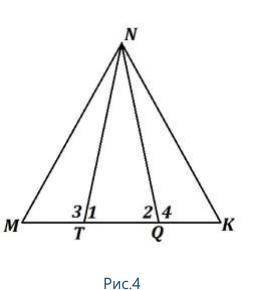
Высота треугольника MNK
является медианой треугольника TNQ,
MT=QK (рис.4). Докажите, что треугольник
MNK равнобедренный. Найдите ∠3, если
∠2 + ∠1 − ∠4 = 30°.
Другие вопросы по теме Геометрия
Популярные вопросы
- Водном ряду 9 стульев. на сколько меньше стульев в трех рядах, чем в пяти таких...
2 - Откуда в санкт петербурге в подинь издаётсч пушичный выстрил...
1 - Артур хочет купить машинку стоит они одинаково если он купит 7 машины у него...
3 - Разложите на множители pg-2g+8-2p²!...
3 - Составь словарный диктант запиши по 3 слова на каждую орфограмму безударные...
2 - Вычислите объём куба с ребром: 2 целых 1/5...
1 - Людии покрытосемянные растения господствующая группа растений на земле....
1 - Картина з.е.серебряковой девочки у рояля.какое музыкальное произведение она...
1 - Туриств поднялся в первый день на 750 метров а во второй день они осили две...
1 - Строение клетки человека и ее органоидов...
2
Відповідь:
110°
Пояснення:
Так как высота треугольника MNK и треугольника TNQ, потому что TQєМК,
является медианой треугольника TNQ, то треугольник TNQ - равнобедренный и NQ=TN, углы при основании равны ∠2 =∠1 .
Так как углы ∠3 и ∠4 − смежные углам ∠1 и ∠2, соответственно, то ∠3=∠4
Так как MT=QK , ∠3=∠4 и NQ=TN то по первому признаку треугольники МTN и NQК равны -> NМ=КN -> треугольник MNK равнобедренный.
∠2 + ∠1 − ∠4 = 30°.
∠2 =∠1=180°-∠4
360°- 2∠4 - ∠4=30°
360°-30°=3∠4
∠4=330°÷3
∠4=110°
∠3=∠4=110°