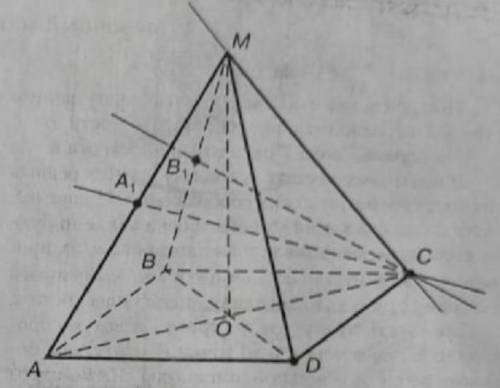
Высота правильной пирамиды МАБСД равна стороне основания. Считая АБ = а. Найдите расстояние от точки Д до следующих прямых а) МС
б) Б1С точка Б1, которой является серединой рёбра МБ
в) А1С точка А1, которой является серединой рёбра МА
Другие вопросы по теме Геометрия
Популярные вопросы
- Какое будет проверочное слово к слову сегодня?...
3 - Почему в весеннем лесу снег тает дольше чем на поле ? какое это имеет значение...
2 - Какое произведение тождественно равно выражению 3m2+9m...
2 - 5x-3×(2x+5)=-x+1 6+9x=4x-1 4x+2=8×(x-5) с уравнением 7 класс...
2 - Рост 160 см,нужно перевести в аршины...
3 - Составь вопросы и ответы на них .exampl: you/in summer/do/to walk/like? - do...
1 - 1. какие теории происхождения человека существуют сегодня? 2. какая из этих...
1 - получения кислорода (дайте ответ как можно скорее) 15...
2 - Нужен диалог трёх человек где они знакомятся сделать!...
1 - Решите 25 5 букв алфавита закодированы различной длины a(-+), b(++), c(+-)...
3
Поместим пирамиду в систему координат вершиной В в начало, ВА по оси Ох, ВС по оси Оу.
Пусть сторона основания и высота равны 1.
Координаты точек: А(1; 0; 0), В(0; 0; 0), С(0; 1; 0), Д(1; 1; 0), М(0,5; 0,5; 1).
В1(0,25; 0,25; 0,5), А1(0,75; 0,25; 0,5).
Векторы. МС: (-0,5; 0,5; -1),
В1С(-0,25; 0,75; -0,5),
А1С(-0,75; 0,75; -0,5).
Уравнения прямых.
МС: (x-0.5)/(-0.5) = (y-0.5)/0.75 = (z-0.5)/-1.
B1C: (x-0.25)/(-0.25) = (y-0.25)/0.75 = (z-0.5)/(-0.5).
A1C: x/(-0.75) = (y-1)/0.75 = z/((-0.5).
1) Находим расстояние от точки Д до прямой МС:
s = -0.5; 0.5; -1 - направляющий вектор прямой;
M = 0.5; 0.5; 1 - точка лежащая на прямой.
Тогда
M0M = {Mx - M0x; My - M0y; Mz - M0z} = 0.5 - 1; 0.5 - 1; 1 - 0 = -0.5; -0.5; 1
Площадь параллелограмма лежащего на двух векторах M0M и s:
S = |M0M × s|
M0M × s =
I j k
-0.5 -0.5 1
-0.5 0.5 -1 =
= i -0.5·(-1) - 1·0.5 - j -0.5·(-1) - 1·(-0.5) + k -0.5·0.5 - (-0.5)·(-0.5) =
= i 0.5 - 0.5 - j 0.5 + 0.5 + k -0.25 - 0.25 =
= 0; -1; -0.5
Зная площадь параллелограмма и длину стороны найдем высоту (расстояние от точки до прямой):
d = |M0M×s||s| = √(0² + (-1)² + (-0.5)²)) /√((-0.5)² + (0.5)² + (-1)²) = √1.25/√1.5 = √(5/6) = √30/6 ≈ 0.91287.
2) Находим расстояние от точки Д до прямой В1С:
s = -0.25; 0.75; -0.5 - направляющий вектор прямой;
B = 0.25; 0.25; 0.5 - точка лежащая на прямой.
Тогда
M0M1 = {M1x - M0x; M1y - M0y; M1z - M0z} = 0.25 - 1; 0.25 - 1; 0.5 - 0 = -0.75; -0.75; 0.5
Площадь параллелограмма лежащего на двух векторах M0M1 и s:
S = |M0M1 × s|
M0M1 × s =
i j k
-0.75 -0.75 0.5
-0.25 0.75 -0.5 =
= i -0.75·(-0.5) - 0.5·0.75 - j -0.75·(-0.5) - 0.5·(-0.25) + k -0.75·0.75 - (-0.75)·(-0.25) =
= i 0.375 - 0.375 - j 0.375 + 0.125 + k -0.5625 - 0.1875 =
= 0; -0.5; -0.75
Зная площадь параллелограмма и длину стороны найдем высоту (расстояние от точки до прямой):
d = |M0M1×s||s| = √(0² + (-0.5)² + (-0.75)²)/√((-0.25)² + (0.75)² + (-0.5)²) = √0.8125/√0.875 = √(13/14) = √182/14 ≈ 0.96362.
3) Находим расстояние от точки Д до прямой В1С:
s = -0.75; 0.75; -0.5 - направляющий вектор прямой;
C = 0; 1; 0 - точка лежащая на прямой.
Тогда
M0M1 = {M1x - M0x; M1y - M0y; M1z - M0z} = 0 - 1; 1 - 1; 0 - 0 = -1; 0; 0
Площадь параллелограмма лежащего на двух векторах M0M1 и s:
S = |M0M1 × s|
M0M1 × s =
i j k
-1 0 0
-0.75 0.75 -0.5 =
= i 0·(-0.5) - 0·0.75 - j -1·(-0.5) - 0·(-0.75) + k -1·0.75 - 0·(-0.75) =
= i 0 - 0 - j 0.5 - 0 + k -0.75 - 0 =
= 0; -0.5; -0.75
Зная площадь параллелограмма и длину стороны найдем высоту (расстояние от точки до прямой):
d = |M0M1×s||s| = √(0² + (-0.5)² + (-0.75)²)/√((-0.75)² + (0.75)² + (-0.5)²) = √0.8125/√1.375 = √(13/22) = √286/22 ≈ 0.76871.