1. Геометрия
  2. Высота правильной четырехугольной

Высота правильной четырехугольной пирамиды равна 6√3 см, а боковое ребро наклонено к плоскости основания под углом 60º.
• найдите боковое ребро пирамиды.
• найдите площадь боковой поверхности пирамиды.
Подробно

olya2399 olya2399    3   16.03.2020 18:47    18

Ответы
mivliev38p08iax mivliev38p08iax  11.10.2020 23:16

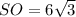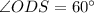Поскольку четырехугольная пирамида правильная, то в её основании служит квадрат. По условию, SO=6\sqrt{3} см и \angle ODS=60^\circ.

Найдём боковое ребро пирамиды из прямоугольного треугольника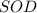 SOD, т.е.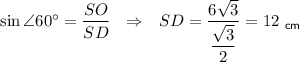 \sin \angle 60^\circ =\dfrac{SO}{SD}~~\Rightarrow~~ SD=\dfrac{6\sqrt{3}}{\dfrac{\sqrt{3}}{2}}=12~_{\sf cm}

\angle OSD=90^\circ -\angle ODS=30^\circ . Против угла 30° катет в два раза меньше гипотенузы, т.е. OD=\dfrac{SD}{2}=6 см. Тогда BD=2OD=12 см.

AD=\dfrac{BD}{\sqrt{2}}=\dfrac{12}{\sqrt{2}}=6\sqrt{2} см

OE - радиус вписанной окружности: OE = AD/2 = 3√2 см.

Найдем апофему SE: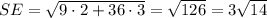 SE=\sqrt{9\cdot 2+36\cdot 3}=\sqrt{126}=3\sqrt{14} см.

S_{bok}=\dfrac{1}{2}P_o\cdot SE=\dfrac{1}{2}\cdot 4\cdot 6\sqrt{2}\cdot 3\sqrt{14}=72\sqrt{7} см²


Высота правильной четырехугольной пирамиды равна 6√3 см, а боковое ребро наклонено к плоскости основ
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
dayanocha0080 dayanocha0080  22.05.2019 07:20
Записать уравнение сферы , проходящей через a(5: 3: 1: ) и с центром о(0; 0; 0)....
вита4321 вита4321  22.05.2019 07:20
Найдите угол м треугольника мрк ,если рк=8,км=6 ,...
lilia822 lilia822  22.05.2019 07:20
Из вершины прямого угла прямоугольного треугольника с катетом 9 см и гипотенузой 15 см проведен перпендикуляр данной 5.4 см к плоскости треугольника. найдите расстояние от...
Tata270204 Tata270204  22.05.2019 07:20
Следствие из аксиом. определения скрещивающихся прямых и параллельности двух плоскостей,...
Katyha028272819 Katyha028272819  23.11.2020 18:58
ДОКАЖИТЕ ЧТО ТРЕУГОЛЬНИКИ ABC и A1B1C1 РАВНЫ...
пельмешик2 пельмешик2  23.11.2020 18:58
Что значит можно ли утверждать в геометрии? Подскажите интересует вопрос касательно термина в предложении типа можно ли утверждать . Если к примеру у нас есть задача:Прямые...
KarenXacul80 KarenXacul80  23.11.2020 18:58
стороны парал-ма равны 4 и 7 см , а угол между ними 30 (градусов) Найти S парал-ма (решите и желательно решение напишите...
sofa4565787 sofa4565787  15.12.2020 22:43
Решить по рисункуjjddjsksksksk​...
Дарчик1 Дарчик1  15.12.2020 22:46
Треугольники ABC и МКР равны и оба равнобедренные. КР = 10 см, периметр треугольника ABC равен 26 см. Найдите стороны МК и МР треугольника МКР.​...
emilinloveTV emilinloveTV  05.06.2019 22:00
Вкакой из координатных четвертей пересекаются графики уравнений 4х-у=5 и 8х+2у=7?...

Популярные вопросы