Высота cd прямоугольного треугольника авс, проведённая из вершины прямого угла, равна 4 см. известно что она делит гипотенузу на отрезки ,один из которых равен 4 корней из 3 см. найдите градусные меры острых углов треугольника авс.
Другие вопросы по теме Геометрия
Популярные вопросы
- Что в жизни надежней и выгодней: иметь или уметь...
1 - Что такое чернозём? где образуется чернозём? какая польза от чернозёма?...
1 - Как пишется слово забегаю и добегаю -слитно или раздельно?...
2 - Цинк взаимодействует с каждом веществом группы: 1) водород, сульфат меди...
1 - Слово сметана разобрать там корень суфикс окончание...
3 - Написать заметку в газету на тему: что важнее: говорить человеку о его достоинствах...
2 - Морфологический разбор слова-называется(3)...
3 - Какой участок рефлекторной дуги нужно удалить у собаки что бы выработанные...
1 - По какой местности протекает река днепр...
2 - Несколько предложений о том,какое впечатление на меня произвел рассказ маленький...
2
Вариант решения.
Найдем второй отрезок гипотенузы.
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.⇒
СD²=АD•ВD
16=4√3•BD
BD=16:4√3=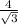
Из ∆ АВD: ∠САD= arctg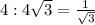 , т.е. 30°
, т.е. 30°
Из ∆ ВСD ∠СВD=arctg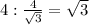 , т.е.60°
, т.е.60°