ВЫРУЧИТЕ

Даны точки А(2;3), В(5;2), С(-2;0), Д(723;4). Найдите:

Скалярное произведение векторов АВ и АС;

Косинус угла ϕ между векторами АВ и АС; и величину угла ϕ в градусах

Ответы

TEMOXAA 06.08.2020 13:48

Объяснение:

А(2;3), В(5;2),С(-2;0)

Найдем для начала координаты векторов

1. АВ =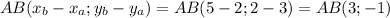 AB(x_b-x_a;y_b-y_a) = AB(5-2;2-3)=AB(3;-1)

2. AC =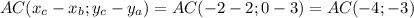 AC(x_c-x_b;y_c-y_a) = AC(-2-2;0-3) = AC(-4;-3)

Найдем теперь скалярное произведение векторов по координатам. Для этого нужно перемножить соответствующие координаты векторов и сложить это.

3.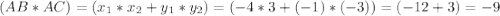 (AB*AC) = (x_1*x_2 + y_1*y_2) = (-4*3 + (-1)*(-3)) = (-12+3)= -9 , где индекс 1 относится к вектору АВ, а индекс 2 к вектору АС.

Теперь найдем модули (длины векторов АВ и АС. Для этого нужно воспользоваться формулой

d=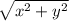 $\sqrt{x^2 + y^2}$ где x и у соответствующие координаты вектора .

$d_1=\sqrt{x_1^2+y_1^2} = \sqrt{3^2+(-1)^2} = \sqrt{10}$ - длина (модуль) вектора АВ

$d_2 = \sqrt{x_2^2+y_2^2} = \sqrt{(-4)^2+(-3)^2} = 5$ - Длина (модуль) АС

Теперь

$cos\alpha =\frac{(AB*AC)}{|AB|*|AC|} = -\frac{9}{5*\sqrt{10} }$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

Bossip 19.10.2019 21:55

Weltrаum 19.10.2019 21:52

lyuda00777 19.10.2019 21:48

Dashad27 19.10.2019 21:33

КРИЛЛ2000 19.10.2019 21:31

ntazhibaevaa 21.12.2020 11:20

vshapovalova21 29.05.2019 19:50

vaki3 29.05.2019 19:50

ыфыфыф553 29.05.2019 19:50

Zvezdo4kaKatty 29.05.2019 19:50

ВЫРУЧИТЕДаны точки А(2;3), В(5;2), С(-2;0), Д(723;4). Найдите:Скалярное произведение векторов АВ и АС;Косинус угла ϕ между векторами АВ и АС; и величину угла ϕ в градусах​