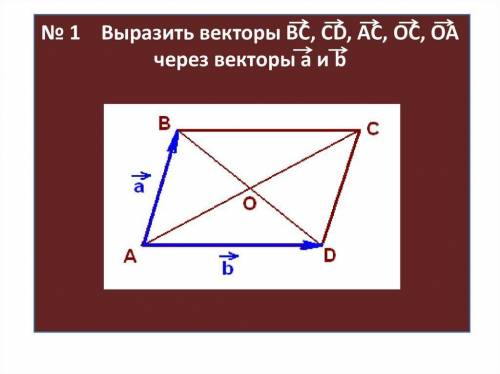
Выразить векторы BC CD AC OC OA через векторы a и b
Другие вопросы по теме Геометрия
Популярные вопросы
- В1. с уменьшением порядкового номера в а(главных)подгруппах периодической...
1 - Укажите период когда земли входили в состав великого княжества литовского...
2 - Решить ) 3. количество населения г. киева составляет 2815,8 тыс....
3 - 9; −5; −1; … найдите 8-й член этой прогрессии....
2 - Тибул залез на кольцо,окружавшее фонарь. ничего! -кричали гвардейцы.-он...
1 - Для прыжка в длину с разбега используется дорожка длиной около: a)...
3 - Придумать вопросы к словам : сеть, норма, успех, старуха, налог,...
2 - Запишіть адресу комірки, яка знаходиться на перетині р та рядка 25...
1 - Можете решить 5 номеров, не трудных 30 !...
1 - Какая величина измеряется в н*кг/па*м^2...
2
Начнем с вектора BC. Обратите внимание, что вектор BC выглядит как разность векторов B и C. Мы можем выразить его следующим образом:
BC = B - C
Теперь обратимся к вектору CD. Мы можем видеть, что вектор CD выглядит как разность векторов C и D:
CD = C - D
Далее рассмотрим вектор AC. Мы можем заметить, что вектор AC выглядит как сумма векторов AB и BC:
AC = AB + BC
Теперь перейдем к вектору OC. Вектор OC является суммой векторов OA и AC:
OC = OA + AC
И, наконец, рассмотрим вектор OA. Нам известно, что вектор OA равен сумме векторов OB и BA:
OA = OB + BA
Таким образом, мы выразили векторы BC, CD, AC, OC и OA через векторы a и b пошагово, используя заданные отношения этих векторов.
Надеюсь, это пояснение помогло вам понять, как выразить данные векторы. Если у вас возникнут еще вопросы, не стесняйтесь задавать их!