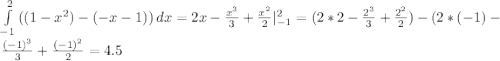Вычислите площадь фигуры, ограниченной графиками функций: y=1-x^2, y=-x-1.
Другие вопросы по теме Геометрия
Популярные вопросы
- Як називаються процеси що повторюються?...
2 - На стороне AB треугольника ABC как на диаметре построена окружность...
1 - У рівнобедреному трикутнику кути при основі рівні — по 45°. Який це...
1 - Які три мовні групи населяють європу?...
1 - Знайдіть сторону рівностороннього трикутника, якщо його медіана дорівнює...
1 - Укажите дату и последовательность!...
2 - Олово встречается в природе в виде минерала касситерита.рассчитайте...
3 - 23 26/37+ 7 18/19 - 4 27/36 ...
3 - Чи актуальні байки щука. жаба і віл . муха і бджола...
2 - чому греко католицьке духівництво відігравало одну з провідних ролей...
2
Sfig=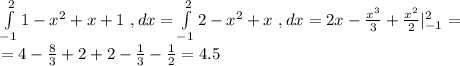
Вот график и область фигуры:
Парабола пересекается с прямой в точках -1 и 2. Она находится выше прямой, значит вычитаем из неё прямую
S =