1. Геометрия
  2. Вычислить площадь фигуры,

Вычислить площадь фигуры, заключенной между графиками функций y=2sqrt(x) и y=x сделать чертеж.

zalinairina9 zalinairina9    2   22.05.2019 10:00    1

Ответы
pumpus pumpus  17.06.2020 15:53

Площадь фигуры которую необходимо вычислить изображена на рисунке во вложении, найдем точки пересечения графиков:

2\sqrtx=x

4x=x^2

4x-x^2=0

x=0

x=4

Вычислим площадь фигуры применяя определенный интеграл:

\int\limits^4_0 {f(x_1)-f(x_2)} \, dx =\int\limits^4_0 {x-2\sqrt{x}} \, dx =(\frac{x^2}{2}-\frac23x^{\frac{3}{2}})|_0^4=\frac{4^2}{2}-\frac23*2^3=8-\frac{16}{3}=\frac{8}{3}

ответ: площадь равна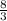 \frac{8}{3} квадратных единиц


Вычислить площадь фигуры, заключенной между графиками функций y=2sqrt(x) и y=x сделать чертеж.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
esergee2012 esergee2012  16.09.2019 23:20
Втреугольнике авс проведена биссектриса вд точка д делит сторону ас на отрезки ад и дс соответсктвенно равные 3 см и 5 см найдите сторону ав если сторона вс равна 10см...
laura35 laura35  16.09.2019 23:20
Основание равнобедренного треугольника в 3 раза меньш боковой стороны а его периметр равен 28 см.найдите стороны треугольника....
Арина2531 Арина2531  16.09.2019 23:20
Биссектриса bd делит сторону ac треугольника abc на отрезки ad и cd, равные соответственно 7см и 10,5см. найдите периметр треугольника abc, если известно, что ab=9см....
akhmetova1 akhmetova1  23.09.2019 14:00
11.8 найдите периметр квадрата, описанного около окружности радиуса 13 см...
anyyy001 anyyy001  21.08.2019 21:00
На рисунке 44 угол 1 равен углу 2 угол 2 равен углу 3 докажите что прямые a и c параллельны...
ilyu777 ilyu777  26.09.2019 01:40
50 мне нужно решение и средняя линия прямоугольной трапеции равна 12 см, а высота, проведенная из вершины тупого угла, делите ее основу для отрезки, длина которых относятся как...
xuligan79 xuligan79  26.09.2019 01:40
Втреугольнике авс,de cредняя линия.de =5см.найти ab...
X1ТихийСнайпер1X X1ТихийСнайпер1X  26.09.2019 01:40
Вычеслите основание равнобедренного треугольника если высота равна 15 см, а боковая сторона 17 см...
Olegg9 Olegg9  26.09.2019 01:40
Выберите верное утверждение а)куб является прямоугольным параллелепипед ом б)ребра куба выходящие из одной вершины имеют разную длину в) объём куба можно найти по формуле v=a³...
Lunit Lunit  30.01.2021 14:48
1) Чему равна диагональ квадрата со стороной 12 см? 2) Найдите сторону квадрата, если его диагонали равна 8 см. 3) К прямой a проведены наклонные AB=17 см, AC=10 см и перпендикуляр...

Популярные вопросы