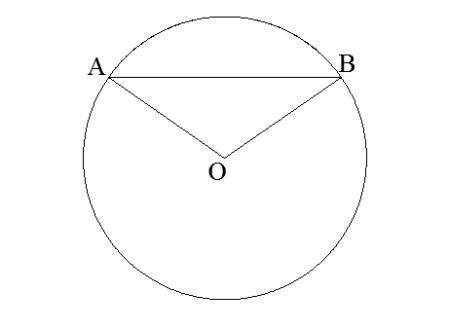
Вычисли углы треугольника AOB, если ∪AnB= 153°, O — центр окружности. ∢ ABO=
∢ BAO=
∢ AOB=

Чтобы вычислить углы треугольника AOB, нам нужно использовать свойства треугольника и окружности.

1. Сначала обратимся к центральному углу ∪AnB, который равен 153°. Это угол, который опирается на дугу AnB. По свойству центрального угла, мы знаем, что угол между двумя лучами, исходящими из центра окружности и пересекающими окружность, в два раза больше угла на пересекаемой дуге. Таким образом, дуга AnB равна (153° / 2) = 76.5°.

2. Теперь обратимся к треугольнику AOB. У нас есть три угла, ∢ABO, ∢BAO и ∢AOB, которые обозначены на диаграмме.

3. Зная, что сумма углов треугольника равна 180°, мы можем записать уравнение:
∢ABO + ∢BAO + ∢AOB = 180°

4. Также мы знаем, что ∢ABO = ∢BAO, так как это углы при основании равнобедренного треугольника.

5. Подставим эту информацию в уравнение:
∢ABO + ∢ABO + ∢AOB = 180°

6. Теперь заменим ∢ABO на х (назовем его переменной):
x + x + ∢AOB = 180°
2x + ∢AOB = 180°

7. У нас есть еще одна информация — дуга AnB равна 76.5°. Так как угол AOB стоит на этой дуге, мы можем записать уравнение связи между углом AOB и дугой AnB:
∢AOB = (дуга AnB) / 2 = 76.5° / 2 = 38.25°

8. Теперь подставим эту информацию в уравнение:
2x + 38.25° = 180°

9. Вычтем 38.25° из обоих сторон уравнения:
2x = 180° - 38.25°
2x = 141.75°

10. Разделим обе стороны на 2:
x = 141.75° / 2
x = 70.875°

11. Таким образом, мы получили значение ∢ABO (и ∢BAO), которое равно 70.875°.

12. Теперь мы можем вычислить значение ∢AOB, подставив его в исходное уравнение:
2x + ∢AOB = 180°
2(70.875°) + ∢AOB = 180°
141.75° + ∢AOB = 180°
∢AOB = 180° - 141.75°
∢AOB = 38.25°

Таким образом, углы треугольника AOB равны:
∢ABO = ∢BAO = 70.875°
∢AOB = 38.25°