Вычисли третью сторону треугольника, если две его стороны соответственно равны 4 см и 8 см, а угол между ними равен 120°. ответ: третья сторона равна ?
Другие вопросы по теме Геометрия
Популярные вопросы
- Промінь BL поділяє кут ABC на два кути. Знайдіть кут ABL, якщо кут...
1 - 2. Substitute the underlined parts of the sentences by Gerundial...
3 - Место и время действия в произведении поучение владимира Мономаха...
3 - Дан прямоугольный параллелепипед ABCDA B C D1. Найдите рассто яние...
1 - - Кто из правителей ввел единый календарь на основе системы, разработанной...
1 - Плоские углы при вершине А пирамиды - прямые, АД=АВ=АС, Sполн=12+4v3....
1 - . Вчера поставил телефон Samsung j1 prime на зарядку, из гнезда пошла...
3 - Сколько гектаров каждая из площадей если общая площадь равна 72 гектаров...
2 - Кто решит мой пример,с тем спишусь и выполню любое желание :))) Пример:...
3 - До іть будьласка, це дуже терміново....
1
ответ: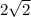 см.
см.
Теорема косинусов имеет следующий вид:
c^2 = a^2 + b^2 - 2ab*cos(C)
Где c - третья сторона треугольника, a и b - две известные стороны, C - угол между этими сторонами.
В нашем случае, известны стороны a = 4 см и b = 8 см, а угол C = 120°. Нам нужно найти длину третьей стороны c.
Подставим известные значения в формулу теоремы косинусов:
c^2 = 4^2 + 8^2 - 2 * 4 * 8 * cos(120°)
Выполним вычисления.
Сначала найдем cos(120°). Для этого мы можем воспользоваться известным фактом, что cos(120°) = cos(360° - 120°) = cos(240°). Угол 240° лежит в третьем квадранте, где косинусы отрицательны, поэтому cos(240°) = -cos(60°). А cos(60°) = 1/2. Поэтому cos(120°) = -1/2.
Теперь подставим известные значения:
c^2 = 4^2 + 8^2 - 2 * 4 * 8 * (-1/2)
Продолжим вычисления:
c^2 = 16 + 64 + 64 = 144
Теперь найдем корень из полученного значения:
c = sqrt(144)
c = 12 см
Таким образом, третья сторона треугольника равна 12 см.