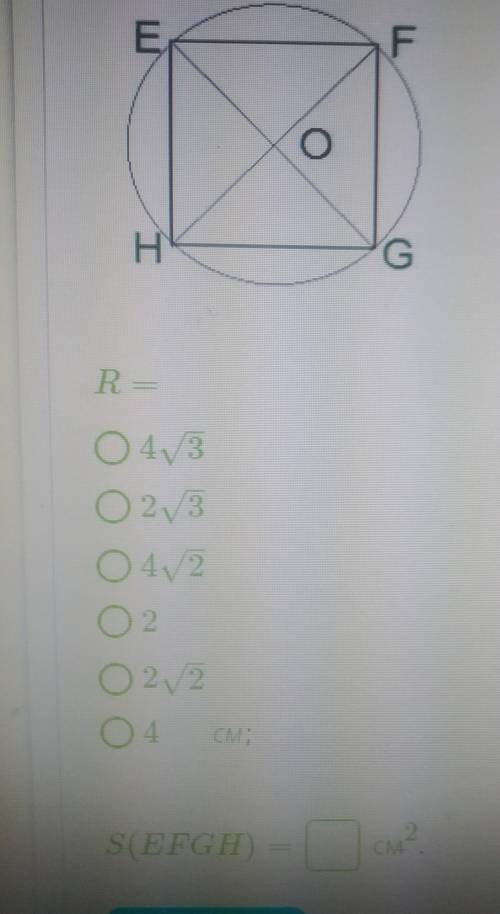
Вычисли неизвестные величины, если EFGH - квадрат со стороной 4 см. ​

Для вычисления неизвестных величин в этой задаче, нам необходимо использовать свойства квадрата.

Исходя из задания, сторона квадрата EFGH равна 4 см. Это означает, что все стороны квадрата одинаковые.

Давайте рассмотрим задание подробнее и определим неизвестные величины.

На задании изображены следующие отрезки:

1. AB - это одна из сторон квадрата. Так как сторона квадрата равна 4 см, то длина отрезка AB также будет равна 4 см.

2. AC - это диагональ квадрата. Диагональ квадрата делит его на два равных прямоугольных треугольника. Зная длину одной стороны квадрата (4 см), мы можем вычислить длину диагонали при помощи теоремы Пифагора.

Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Давайте обозначим длину диагонали как d. Мы знаем длину одной стороны квадрата (4 см) и расстояние от угла D до середины стороны AB, которое равно половине длины стороны (2 см). Таким образом, мы можем составить уравнение: d^2 = 4^2 + 2^2.
Решим это уравнение, сначала вычислив сумму квадратов: 4^2 = 16 и 2^2 = 4. Затем, сложив эти результаты, получим: 16 + 4 = 20. Теперь мы знаем, что d^2 = 20. Чтобы найти d, возьмем квадратный корень из 20. Приближенно, значение диагонали будет равно 4.47 см.

3. АE - это другая диагональ квадрата. Она также будет равна 4.47 см, так как спецификации квадрата не меняются в зависимости от направления проведения диагоналей.

4. BF - это перпендикуляр, проведенный от точки B к стороне AE. Нам не дана информация о его длине или других свойствах, поэтому мы не можем найти его значение на основе предоставленных данных.

5. EF - это сторона треугольника EBF. Для ее вычисления нам требуется найти значение BF. Опять же, мы не можем его найти без дополнительных данных.

Таким образом, после анализа задачи мы можем найти следующие значения:

- Длина отрезка AB: 4 см.
- Длина диагоналей AC и AE: 4.47 см.

Однако, данные недостаточны для определения длины отрезка BF или стороны EF треугольника EBF. Для этого нам понадобятся дополнительные сведения о свойствах фигуры или другие известные величины.