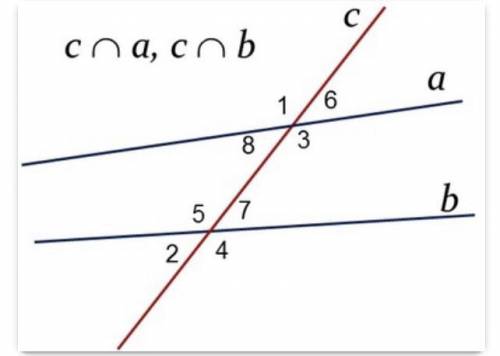
Выберите верные утверждения ∠7 и ∠6 - соответственные углы;
∠7 и ∠1 - накрест лежащие углы;
∠2 и ∠4 - смежные углы;
∠3 и ∠7 - односторонние углы;
∠1 и ∠3 - вертикальные углы;
∠5 и ∠1 - односторонние углы;
∠5 и ∠3 - накрест лежащие углы

7 и 1 накрест лежащие правильно

3 и 7 односторонние правильно

5 и 1 односторонние правильно

и кажеться 5 и 3 тоже правильно

Для решения данной задачи необходимо знать определения различных типов углов.

1. Соответственные углы:
- Соответственные углы - это пара углов, которые находятся на одной прямой и разделяются параллельными прямыми либо пересекающимися прямыми.

Исходя из этого определения, у нас есть две пары углов, а именно ∠7 и ∠6, и ∠7 и ∠1.
- Угол ∠7 и угол ∠6 расположены на прямой CD, но не находятся на одной прямой с углом ∠6, поэтому они не являются соответственными углами.
- Угол ∠7 и угол ∠1 расположены на прямой CD, находятся на одной прямой с углом ∠1 и разделяются параллельными прямыми AB и CD, поэтому они являются соответственными углами.

Итак, верное утверждение: ∠7 и ∠1 - соответственные углы.

2. Накрест лежащие углы:
- Накрест лежащие углы - это пара углов, которые являются внутренними или внешними углами, образованными пересекающимися прямыми.

Исходя из этого определения, у нас есть две пары углов, а именно ∠7 и ∠6, и ∠5 и ∠3.
- Угол ∠7 и угол ∠6 находятся на разных прямых (AC и BD), они не пересекаются, поэтому они не являются накрест лежащими углами.
- Угол ∠5 и угол ∠3 находятся на разных прямых (AC и BD), пересекаются на точке C, поэтому они являются накрест лежащими углами.

Итак, верное утверждение: ∠5 и ∠3 - накрест лежащие углы.

3. Смежные углы:
- Смежные углы - это пара углов, которые имеют общую вершину и одну сторону, но не пересекаются.

Исходя из этого определения, у нас есть две пары углов, а именно ∠2 и ∠4, и ∠1 и ∠3.
- Угол ∠2 и угол ∠4 не имеют общей вершины, поэтому они не являются смежными углами.
- Угол ∠1 и угол ∠3 имеют общую вершину D и одну сторону AD, поэтому они являются смежными углами.

Итак, верное утверждение: ∠1 и ∠3 - смежные углы.

4. Односторонние углы:
- Односторонние углы - это пара углов, которые имеют общую вершину и одну сторону, и их другая сторона продолжается прямолинейно по обе стороны.

Исходя из этого определения, у нас есть две пары углов, а именно ∠3 и ∠7, и ∠5 и ∠1.
- Угол ∠3 имеет сторону DC и продолжается прямолинейно по стороне CD, а угол ∠7 имеет сторону BC и продолжается прямолинейно по стороне CD, поэтому они являются односторонними углами.
- Угол ∠5 имеет сторону BC и продолжается прямолинейно по стороне CD, а угол ∠1 имеет сторону AD, не продолжающуюся прямолинейно по стороне CD, поэтому они не являются односторонними углами.

Итак, верное утверждение: ∠3 и ∠7 - односторонние углы.

5. Вертикальные углы:
- Вертикальные углы - это пара углов, которые имеют общую вершину и стороны являются продолжением друг друга.

Исходя из этого определения, у нас есть две пары углов, а именно ∠1 и ∠3, и ∠6 и ∠4.
- Угол ∠1 и угол ∠3 имеют общую вершину D и стороны AB и CD, которые являются продолжением друг друга, поэтому они являются вертикальными углами.
- Угол ∠6 и угол ∠4 не имеют общей вершины, поэтому они не являются вертикальными углами.

Итак, верное утверждение: ∠1 и ∠3 - вертикальные углы.

В результате, верные утверждения:
- ∠7 и ∠1 - соответственные углы;
- ∠3 и ∠7 - односторонние углы;
- ∠1 и ∠3 - вертикальные углы;
- ∠5 и ∠3 - накрест лежащие углы.