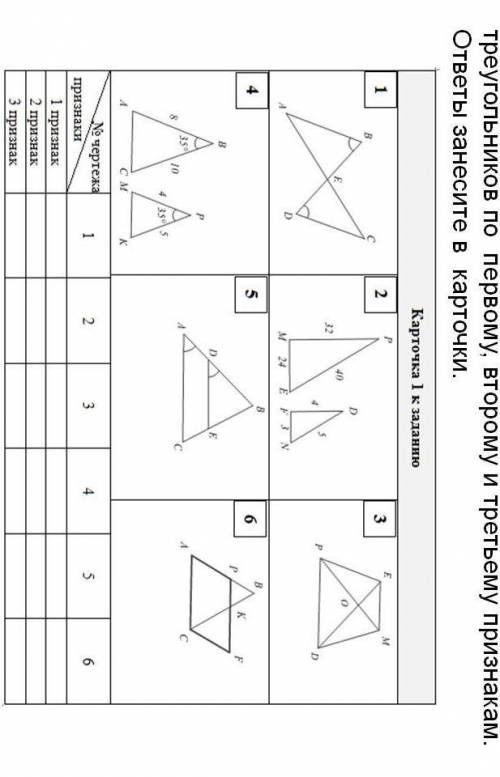
Выберите номера чертежей подобных треугольников по первому, второму и третьему признакам. ответы занесите в карточки.
Другие вопросы по теме Геометрия
Популярные вопросы
- 1. Какое значение слова осенить2. Подберите синонимы к словам...
3 - Синтаксический разбор предложения Голые деревья замерли в глубоком...
3 - Какие изменения были в биологических науках в XXв?...
2 - 94. Көбейтудің үлестірімділік қасиетін пайдаланып, есепті өрнек...
3 - Электрический самовар имеет два нагревателя: первый мощностью...
1 - 2.14. Түзуде: а) 3 нүкте; ә) 4 нүкте; б) 5 нүкте; в)* пнүкте белгі-...
1 - Ұ ү ө дыбыстары айтылғанымен, жазылмау себебін түсіндірдіңіз...
1 - Ұқсастығы мен айырмашылығын тап. Патша өкіметінің Еділ-Жайық аймағында...
1 - Подготовьте коллаж к одному из понятий: ум, сила, сердце.Выразите...
1 - Проверьте свои знания 1. Какие изменения происходили в экономике...
3
Первый признак подобия треугольников: Углы треугольников равны попарно.
Анализируя чертежи, мы видим, что у треугольников на чертежах 2 и 4 имеются два равных угла. Значит, треугольники 2 и 4 подходят по первому признаку подобия.
Второй признак подобия треугольников: Отношение длин любых двух сторон одного треугольника равно отношению длин соответствующих сторон другого треугольника.
Для проверки второго признака нам нужно сравнить отношение длин сторон одного треугольника с отношением длин соответствующих сторон другого треугольника. Давайте рассмотрим каждую пару чертежей:
- Треугольники 1 и 3: Отношение длин сторон (4:2 = 2:1) в треугольнике 1 равно отношению длин сторон (6:3 = 2:1) в треугольнике 3. Значит, треугольники 1 и 3 подходят по второму признаку подобия.
- Треугольники 2 и 4: Отношение длин сторон (3:2 = 3:2) в треугольнике 2 равно отношению длин сторон (9:6 = 3:2) в треугольнике 4. Значит, треугольники 2 и 4 также подходят по второму признаку подобия.
Третий признак подобия треугольников: Отрезки, соединяющие соответственные вершины подобных треугольников, делятся на одни и те же отрезки в одних и тех же отношениях.
Для проверки третьего признака нам нужно сравнить отношение длин отрезков, соединяющих соответственные вершины подобных треугольников. Давайте рассмотрим каждую пару чертежей:
- Треугольники 1 и 2: Отношение длин отрезков (2:4 = 1:2) в треугольнике 1 равно отношению длин отрезков (4:8 = 1:2) в треугольнике 2. Значит, треугольники 1 и 2 подходят по третьему признаку подобия.
- Треугольники 2 и 4: Отношение длин отрезков (2:3 = 2:3) в треугольнике 2 равно отношению длин отрезков (4:6 = 2:3) в треугольнике 4. Значит, треугольники 2 и 4 также подходят по третьему признаку подобия.
Окончательно, мы можем сказать, что треугольники 2 и 4 подходят к треугольнику 1 по всем трем признакам подобия.
Ответ: Номера чертежей подобных треугольников по первому, второму и третьему признакам - 2 и 4.