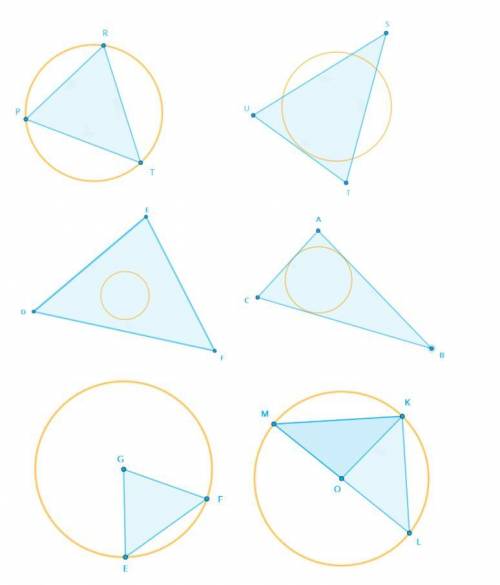
Выбери треугольник, который описан около окружности. EFG
PRT
STU
KLM
ABC
DEF

Выберем треугольник, который может быть описан около окружности. Для этого нужно учитывать определенное свойство окружности, а именно, что углы, образованные при соединении точки окружности с точками треугольника, являются прямыми углами.

Давайте рассмотрим каждый треугольник по отдельности:

1) Треугольник EFG: Он может быть описан около окружности, так как угол EFG является прямым углом.

2) Треугольник PRT: Он не может быть описан около окружности, так как ни один из его углов не является прямым углом.

3) Треугольник STU: Он не может быть описан около окружности, так как ни один из его углов не является прямым углом.

4) Треугольник KLM: Он не может быть описан около окружности, так как ни один из его углов не является прямым углом.

5) Треугольник ABC: Он не может быть описан около окружности, так как ни один из его углов не является прямым углом.

6) Треугольник DEF: Он может быть описан около окружности, так как угол DEF является прямым углом.

Итак, треугольники EFG и DEF могут быть описаны около окружности, так как в них имеются прямые углы.