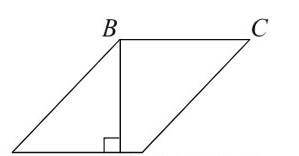
Высота BH ромба ABCD делит его сторону AD на отрезки AH=60 и HD=8 . Найдите площадь ромба.
Другие вопросы по теме Геометрия
Популярные вопросы
- Перевод на пож. stream, waterfall,rainworm,tiger,wolf,piglet....
2 - Эссе на тему я учёный придумайте новый источник энергии,...
3 - Составьте общее уравнение прямой проходящей через точки а(-3; 2)...
1 - Перепиши предложения, вставляя тире, где это нужно. объясни своё...
3 - 25 ! решить ! выражение х^2-9/3х^2-9х...
2 - Где а. де сент-экзюпери попал в аварию? !...
1 - Поезд жолдың 180 км-ін 36 км/сағ қпен, екінші бөлігін 100 км-ді...
3 - 4целых 1/6 * 3целых 3/5=2целых 2/3 *1целая 1/8: 6целых 2/3 20б....
3 - Составить сравнительную характеристику герды и снежной королевы...
2 - Докажите справедливость высказывания критика: «природа у бунина-в...
2
Шаг 1: Найдем длину основания AD.
Так как HD и AH являются равными отрезками, то сумма этих двух отрезков будет равна длине основания AD:
AH + HD = AD
60 + 8 = AD
68 = AD
Шаг 2: Найдем площадь треугольника AHD.
Площадь треугольника можно найти, используя формулу: S = (основание * высота) / 2
В нашем случае, основание треугольника AHD равно AD, а высота треугольника равна HD.
Подставим значения в формулу:
S = (AD * HD) / 2
S = (68 * 8) / 2
S = 544 / 2
S = 272
Шаг 3: Площадь ромба равна удвоенной площади треугольника AHD.
Подставим значение площади треугольника AHD в формулу:
Площадь ромба = 2 * S
Площадь ромба = 2 * 272
Площадь ромба = 544
Ответ: Площадь ромба составляет 544 квадратных единицы.