Ввыпуклом четырехугольнике abcd каждая из диагоналей ac и bd имеет длину 2√5. точки m,n,p,q - середины сторон ab,bc,cd,ad соответственно. найти площадь четырехугольника abcd, если mp+nq=6

 Четырехугольник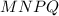  параллелограмм.

Параллелограмм 

 составляет половину площади   четырехугольника  . 

Положим что стороны параллелограмма    , .

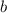Периметр параллелограмма равен сумме диагоналей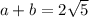  

Положим что диагонали равны     ,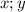   

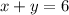
В параллелограмме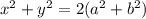        

 Угол между диагоналями параллелограмма  ромба   ,   

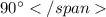
\frac{x^2}{4}+\frac{y^2}{4}-\frac{xy*cos90а}{2}=a^2[/tex] 

 

 \\\\

 

MNPQ - параллелограмм. Smnpq = 0,5*Sabcd. (это известно и доказывать не надо?) MN - средняя линия треугольника АВС и равна 0,5*АС. NP - средняя линия тр-ка ВСD и равна 0,5*BD. Но АС=ВD=2√5(дано). То есть MNPQ - ромб со сторонами, равными √5. Диагонали ромба перпендикулярны и в точке пересечения делятся пополам. Сумма диагоналей этого ромба равна 6 (дано). Значит их полусумма равна 3. Пусть половины диагоналей равны d1 и D1. По Пифагору в любом из прямоугольных треугольников, образованных половинами диагоналей и стороной ромба имеем: (√5)²=d1²+D1² или 5=(3-D1)²+D1². Имеем квадратное уравнение: D1²-3*D1+2=0, имеющее два корня: D1=2 и D1=1. То есть диагонали ромба MNPQ равны 4 и 2. Но тогда площадь этого ромба равна половине произведения диагоналей: Smnpq = (1/2)*D*d = 4. Отсюда искомая площадь Sabcd = 2*Smnpq = 8.
ответ: Sabcd = 8.