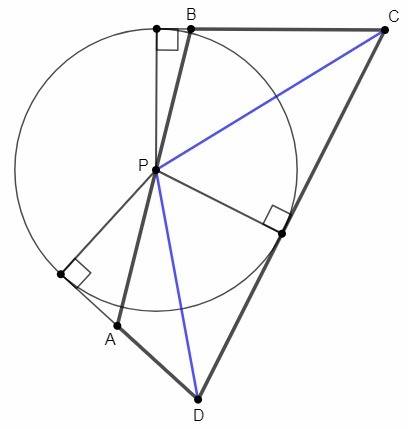
Ввыпуклом четырехугольнике abcd биссектрисы углов c и b пересекаются на стороне ab в точке p докажите , что точка p равноудалена от сторон четырехугольника. из второй части огэ, точно не помню была ли дана сторона, но в голове крутится, что равна 9 или 12(аб). ну,даже если бы сторона не была дана, как ее можно решить?
Ответы
Биссектриса угла - геометрическое место точек, равноудаленных от сторон угла. Точка P лежит на биссектрисе угла BCD, следовательно равноудалена от сторон BC, CD. Точка P лежит на биссектрисе угла CDA, следовательно равноудалена от сторон CD, AD. Таким образом, точка P равноудалена от трех сторон: BC, CD, AD.
ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия
Популярные вопросы
- Решите уравнение . 4*(7-2х)+6(х-1)=-1...
2 - Подобрать число a, такое чтобы уравнение a-(2-2x)=2x-a имело корни...
3 - Синтаксический разбор к слову чудилось ,. буду !...
3 - 23 ! скільки тонн снігу довелось скинути з даху будинку при товщині...
1 - Найдите чисоо если оно состовляет 80% от 40...
3 - Вправление какого князя на руси появились книги? -ярослав мудрый...
1 - Какова основная мысль рассказа на острове сальтрока ? какова тема?...
2 - Периметр квадрата равен 32 кв см вычислите площадь этого квадрата...
2 - Точка a(a; -3) лежит на прямой y=-3/4x+2. чему равен a?...
2 - Мольная доля гидроксида натрия в растворе, содержащем 40 г вещества...
3