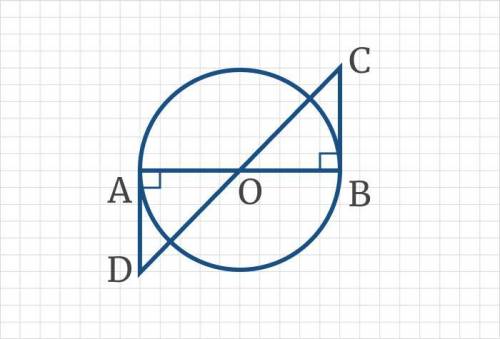
Введите с клавиатуры результат вычислений. На рисунке O – центр окружности, АВ – диаметр окружности. Отрезки АD и ВС, перпендикулярны к отрезку АВ. АВ = 8 см, ОС = 5 см, СВ = 3 см.

Чему равен периметр ∆AOD?

12см

Объяснение:

Для решения этой задачи мы можем использовать знания о геометрических фигурах, а именно, о треугольниках и окружностях.

Первым шагом нужно определить, какие данные даны в задаче и что нам нужно найти. В задаче даны следующие данные:
- Диаметр окружности: AB = 8 см.
- Отрезки AD и ВС перпендикулярны к отрезку АВ.
- Длина отрезка ВС: СВ = 3 см.
- Отрезок ОС: ОС = 5 см.

Нам нужно найти периметр треугольника ∆AOD.

Для начала, нам нужно найти длину отрезка AD. Так как отрезки AD и ВС перпендикулярны к отрезку АВ, мы можем использовать теорему Пифагора, так как треугольник ∆ADB - прямоугольный.

Для этого нужно найти длину отрезка BD. Так как AB - диаметр окружности, он равен 8 см. Также, мы знаем, что OD - радиус окружности, и он равен половине диаметра. То есть, OD = AB/2 = 8/2 = 4 см.

Используя теорему Пифагора, мы можем найти длину отрезка BD:
BD^2 = AB^2 - AD^2
BD^2 = 8^2 - 4^2
BD^2 = 64 - 16
BD^2 = 48

Затем, найдем длину отрезка AD:
AD = √48
AD = 4√3 см

Теперь у нас есть все данные, чтобы найти периметр треугольника ∆AOD. Периметр треугольника вычисляется путем сложения длин всех его сторон.

Периметр треугольника ∆AOD = AD + OA + OD.

Мы уже нашли длину отрезка AD, которая равна 4√3 см.
Также, мы знаем, что ОС = 5 см и ОТ = 3 см.

Теперь нам нужно найти длину отрезка OA. Отрезок OA является радиусом окружности, и он равен ОС + ОТ. То есть, ОА = ОС + ОТ = 5 см + 3 см = 8 см.

Теперь мы можем найти периметр треугольника ∆AOD, сложив длины его сторон:
Периметр ∆AOD = AD + OA + OD = 4√3 см + 8 см + 4 см = 12√3 см + 12 см.

Таким образом, периметр треугольника ∆AOD равен 12√3 см + 12 см.