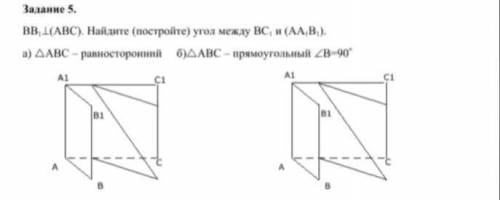
ВВ1 ⊥(АВС). Найдите (постройте) угол между ВС1 и (АА1В1). а)АВС – равносторонний

б)АВС – прямоугольный В=90°

Для решения данной задачи нам необходимо использовать знания о свойствах перпендикуляров и углов. Поскольку ВВ1 ⊥(АВС), мы можем использовать свойство перпендикуляров для того, чтобы утверждать, что угол ВВ1С равен 90 градусов. Теперь перейдем к решению по пунктам. а) АВС – равносторонний треугольник. Это означает, что все стороны треугольника равны между собой. Поскольку треугольник АВС равносторонний, все его углы равны 60 градусов. Отсюда следует, что угол ВАС также равен 60 градусов. Поскольку ВВ1 ⊥(АВС) и ВВ1С — это прямой угол, мы можем утверждать, что угол ВВ1A равен 90-60=30 градусов. Далее построим точку А1 на стороне AV1 так, чтобы она была перпендикулярна AV1. Поскольку ВлевлевоА1 — это прямой угол, у нас есть пара прямых углов ВВ1А=ВлевлевоА1=30 градусов. Итак, угол между ВС1 и (АА1В1) в случае равностороннего треугольника АВС равен 30 градусов. б) АВС – прямоугольный треугольник с углом В = 90 градусов. Мы уже знаем, что угол ВВ1С равен 90 градусов из условия. Поскольку ВВ1 ⊥(АВС) и ВВ1С - это прямой угол, мы можем сделать вывод о том, что угол ВВ1А равен 180-90=90 градусов. Далее построим точку А1 на стороне БС так, чтобы она была перпендикулярна БС. Поскольку у нас есть пара прямых углов ВВ1А=ВлевлевоА1=90 градусов, мы можем сделать вывод о том, что угол между ВС1 и (АА1В1) в случае прямоугольного треугольника АВС равен 90 градусов.