Втреугольнике авс медиана ам перпендикулярна медиане вn. найдите площадь треугольника авс, если ам = 2см, вn = 3см

4см²

Объяснение:

Смотри прикреплённый рисунок.

О - точка пересечения медиан АМ и BN.

Медианы треугольника точкой пересечения О делятся в отношении 2:1, считая от вершины, поэтому BO =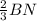 = 2 см, NO = 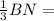1 cм.

Проведём линию MN, соединяющую середины сторон АС и ВС.

MN  = 0.5AB, поскольку MN - средняя линия треугольника.

ΔNMC ~ ΔABC по двум углам (∠С - общий, ∠СMN = ∠СBA как соответственные при MN || AB и секущей ВС)

Коэффициент подобия k = MN: AB = 0,5, поэтому площади ΔNMC и ΔABC относятся, как k² = 0.25.

Тогда площадь трапеции ABMN составляет 0,75 площади ΔABC.

Вычислим площадь трапеции ABMN.

.

.

.