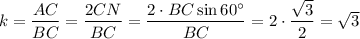Втреугольнике авс (ав = вс) проведены высоты bn и ам, причем bn пересекает ам в точке к.
а) докажите, что треугольники амс и bnc подобны.
б) найдите коэффициент подобия указанных треугольников, если
Другие вопросы по теме Геометрия
Популярные вопросы
- Листики появились на березке. мы летом жили на даче, по тропинке...
1 - Вслове отвёртка орфограмма парного согласного перед другим согласным...
2 - 1. примеры тел,находящихся в состоянии теплового равновесия.поясните...
2 - Как решить в столбик пример 756 раздилить на 7...
2 - Гогда миша отдал маше 4конфеты ,то у них стало конфет поровну.на...
1 - Турист вышел на пункт a и км за 1 три четвёртых часа,затем сделал...
3 - Звуко-буквенный анализ слово объятная...
2 - Расставить порядок действий! 372: 6+123•3-(15+25)•2=? заранее...
1 - Выражение 3by+6y-5b-10/7yb-14y × b²-4/9y²-25 полное решение, ....
2 - Обозначь звуки которые скрываются за двумя последними буквами в...
2
1) У треугольников AMC и BNC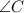 — общий и ∠BNC = ∠AMC, следовательно, ΔAMC ~ ΔBNC по двум углам.
— общий и ∠BNC = ∠AMC, следовательно, ΔAMC ~ ΔBNC по двум углам.
2) Поскольку BN - высота, медиана и биссектриса, то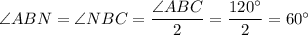
Коэффициент подобия: