Втреугольнике abc угол c равен 90 sinb 4/11 ab 55 найдите ac

Дано:

Треугольник ABC - прямоугольный.

∠C = 90°.

sin ∠B = .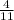

AB = 55.

Найти:

AC = ?

Синус угла прямоугольного треугольника - отношение противолежащего катета к гипотенузе.

В данном случае -

Подставим известные нам значения в формулу -

ответ: 20.

Для начала, давайте разберемся, что нам дано в этой задаче и какие формулы мы можем использовать.

Нам дан треугольник ABC, у которого один из углов, обозначенный буквой "C", равен 90 градусов. Также известно, что sin(B) = 4/11, AB = 55. Задача состоит в том, чтобы найти длину стороны AC.

Для решения данной задачи мы можем использовать тригонометрические соотношения и теорему Пифагора.

Первым шагом давайте воспользуемся теоремой Пифагора, которая гласит: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Таким образом, мы можем записать следующее уравнение:

AC^2 = BC^2 + AB^2.

Мы знаем, что угол C прямой, поэтому сторона AC является гипотенузой треугольника. Также у нас уже есть значение стороны AB.

Затем мы можем использовать формулу для синуса угла B:

sin(B) = противолежащая сторона / гипотенуза.

Из этой формулы мы можем выразить противолежащую сторону:

противолежащая сторона = sin(B) * гипотенуза.

Теперь мы можем воспользоваться этой формулой, чтобы выразить сторону BC:

BC = sin(B) * AC.

Теперь у нас есть два уравнения с двумя неизвестными (AC и BC). Мы можем использовать их, чтобы решить задачу.

Давайте подставим выражение для BC в уравнение Пифагора:

AC^2 = (sin(B) * AC)^2 + AB^2.

Теперь мы можем решить это уравнение:

AC^2 = (4/11 * AC) ^2 + 55^2.

AC^2 = (16/121 * AC^2) + 3025.

(121/121) * AC^2 = (16/121) * AC^2 + 3025.

AC^2 - (16/121) * AC^2 = 3025.

((121 - 16)/121) * AC^2 = 3025.

(105/121) * AC^2 = 3025.

AC^2 = (3025 * 121) / 105.

AC^2 ≈ 3482.62.

AC ≈ √3482.62.

AC ≈ 59.01.

Таким образом, длина стороны AC составляет примерно 59.01 единицы длины.