1. Геометрия
  2. Втреугольнике abc угол

Втреугольнике abc угол c-прямой cos =0,6= bc=12 найдите ab

Veratandashvili Veratandashvili    2   31.03.2019 12:30    12

Ответы
faiarina2016 faiarina2016  27.05.2020 22:18

Если в условии дано что CosA=0.6, то

AB можно найти из определения синуса угла А: SinA=BC/AB, тогда AB=BC/SinA

Надо найти SinA, для этого можно использовать основное тригонометрическое тождество: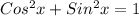 Cos^2x+Sin^2x=1, отсюда получаем, что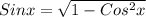 Sinx=\sqrt{1-Cos^2x}

Находим: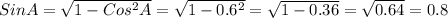 SinA=\sqrt{1-Cos^2A}=\sqrt{1-0.6^2}=\sqrt{1-0.36}=\sqrt{0.64}=0.8

Наконец вычисляем: AB=BC/SinA=12/0.8=15

 

 

 

 Если-же дано что CosB=0.6, то AB=BC/CosB=12/0.6=20

 

ОТВЕТ 15 или 20

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
льоха7 льоха7  09.12.2020 11:04
Постройте сечения с описанием к красным фигурам...
dashamazurkevi dashamazurkevi  09.12.2020 11:02
Решить пошагово, с рисунком. У прямоугольного параллелепипеда грани основания 8 дм и 15 дм. Вычисли высоту параллелепипеда, если известно, что диагональное сечение это квадрат....
yil yil  22.12.2020 06:55
зделать задания все задания...
kassaalevtina kassaalevtina  22.12.2020 06:55
Сторона основания правильной треугольной пирамиды равна 1, боковая площадь поверхности 3. Определить объем пирамиды.​...
неюляша2002 неюляша2002  22.12.2020 06:56
1. На рисунке изображены равные треугольники. Определите, по какому признаку равны треугольники.А)Б)B)Г)​...
Ссика Ссика  22.12.2020 06:56
Выберите полный список изображенных на рисунке углов, внутри которых лежит точка М. 1) AOD, AOC, DOC, BOD;2) AOD, AOC, BOC, BOD;3) AOD, BOC, AOB, BOD.Выберите полный список изображенных...
mishasviderski mishasviderski  22.12.2020 06:56
Стороны треугольника 9 см, 11 см и 12см. Его периметр похож на него более 16 см от периметра треугольника. Стороны второго треугольника находить...
tanyaanya200615 tanyaanya200615  22.12.2020 06:57
Точка А ,имеет координаты (-5,6).Найдите координаты точки А, полученной параллельным переносом точка А,на вектор а (3,2).Из предложенных ответов найдите координаты точки А и сумму...
grange grange  04.03.2021 15:45
нужно (ᗒᗩᗕ) 1) Основания трапеции равны 6 см и 12 см. Чему равенпериметр трапеции, если в неё можно вписать окружность?1 0 см2) Основания трапеции равны 6см и 12см. Чему равен периметр...
51201826 51201826  04.03.2021 15:45
Основание равнобедренного треугольника равен 12 см а боковая сторона равна 5 см. найдите периметр ...​...

Популярные вопросы