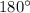Втреугольнике abc стороны ab и bс равны, угол b равен 72°. биссектрисы углов a и c пересекаются в точке m . найдите величину угла amc.
Другие вопросы по теме Геометрия
Популярные вопросы
- Запишите следующие числа в 3 раза подряд и запишите полученное в...
3 - Очем говорится в макбет мценского уезда ? ! заранее...
3 - Определите валентность элементов в соединении na2o co ch4...
2 - Чому гiпербола найпоширенiший художнiй засiб,який використовуеться...
2 - Переведите мне ! внятно и ! the science lab is next to the toilets...
3 - Выступы кристаллического древних платформ на поверхность. как они...
2 - Подайте в метрах на секунду такі значення швидкості руху: 3,6 км/год,...
3 - Объяснение из толкового словаря словам , кокошник, сарафан и пугало....
1 - Как называется высокий женский голос?...
2 - бедная лиза . как в повести выражается отношение автора-рассказчика...
3
ответ: 126
Объяснение:
Сначала посчитаем углы A и С, а они равны, так как треугольник равнобедренный: A=C=(180-72)/2=54
Рассмотрим треугольник АМС:
Угол МАС=54/2=27(т.к. бис-са)
Угол МСА=54/2=27(т.к. бис-са)
Угол АМС=180-уголМАС-уголМСА=180-54=126
Дано :
ΔАВС - равнобедренный (АВ = ВС).
∠В = 72°.
Отрезок АО - биссектриса ∠А.
Отрезок СК - биссектриса ∠С.
Точка М - точка пересечения АО и СК.
Найти :
∠АМС = ?
Углы при основании равнобедренного треугольника равны.Следовательно -
∠А = ∠С.
Сумма внутренних углов треугольника равна 180° (теорема о сумме внутренних углов треугольника).Следовательно -
∠А + ∠В + ∠С = 180°
∠А + ∠С = 180° - ∠В
∠А + ∠С = 180° - 72°
∠А + ∠С = 108°
∠А = ∠С = 108° : 2 = 54°.
Биссектриса угла треугольника - это отрезок, который является биссектрисой угла треугольника.Отсюда -
∠КАМ = ∠МАС = 54° : 2 = 27°
∠АСМ = ∠МСО = 54° : 2 = 27°.
Рассмотрим ΔАМС.
По теореме о сумме внутренних углов треугольника -
∠МАС + ∠АСМ + ∠АМС = 180°
∠АМС = 180° - ∠МАС - ∠АСМ
∠АМС = 180° - 27° - 27°
∠АМС = 126°.
126°.
Объяснение:
Проведём биссектрисы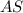 и
и 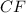 углов
углов 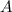 и
и 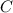 соответственно.
соответственно.
========================================================
Так как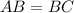

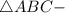 равнобедренный.
равнобедренный.
Сумма внутренних углов треугольника равна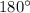 .
.
Так как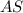 и
и 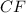 - биссектрисы углов
- биссектрисы углов 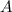 и
и 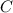 соответственно
соответственно 
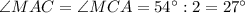
Сумма внутренних углов треугольника равна