Втреугольнике abc проведена средняя линия mk, где m принадлежит ac , k принадлежит ab. площадь треугольника abc равна 64см^2. найдите площадь четырехугольника kbcm.

Треугольник AKM подобен треугольнику ABC по двум углам (угол AKM равен углу ABC и угол AMK равен углу ACB как соответственные углы при параллельных прямых KM и BC - свойство средней линии треугольника) с коэффициентом подобия 2 (то есть BC = 2 * KM). Значит площадь треугольника ABC равна площади треугольника AKM, умноженной на 4 (квадрат коэффициента подобия), отсюда площадь треугольника AKM равна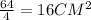 . Тогда площадь трапеции KBCM будет равна разности площадей треугольников ABC и AKM: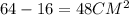

ответ: 48