1. Геометрия
  2. Втреугольнике abc известны стороны

Втреугольнике abc известны стороны ab=15, ac=16, bc=20. в нём проведены биссектрисы bb1 и cc1. прямые b1c1 и bc пересекаются в точке x. найдите bx: xc.

freeSkoM freeSkoM    1   09.05.2019 20:00    28

Ответы
LanaAnn LanaAnn  09.06.2020 18:50

По теореме Минелая:

\dfrac{BX}{XC} \cdot \dfrac{CB_1}{B_1A} \cdot \dfrac{AC_1}{C_1B} =1

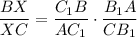
Откуда \dfrac{BX}{XC} =\dfrac{C_1B}{AC_1} \cdot \dfrac{B_1A}{CB_1}

Биссектриса треугольника делит противолежащею сторону на отрезки пропорциональные прилежащим сторонам. Поэтому

\dfrac{C_1B}{AC_1} =\dfrac{BC}{AC} =\dfrac{20}{16}=\dfrac54

И таким же образом

\dfrac{B_1A}{CB_1} =\dfrac{AB}{BC} =\dfrac{15}{20} =\dfrac34

\displaystyle \dfrac{BX}{XC} =\dfrac54 \cdot \dfrac34 =\dfrac{15}{16} =\\\\=1-\dfrac1{16} =1-0,\!0625=0,\!9375

ответ: 0,9375.


Втреугольнике abc известны стороны ab=15, ac=16, bc=20. в нём проведены биссектрисы bb1 и cc1. прямы
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
grigoryanoksan grigoryanoksan  11.06.2019 07:30
Найдите моду ряда 39 54 33 36 20 29 35 50 21 найдите размах ряда 7,2 -0,6 -4,5 6,3 1,1 найдите среднее арифметическое ряда 1,6 4,9 12,4 3,1...
Хайд0тян Хайд0тян  11.06.2019 07:30
Заранее ну надо,. найдите углы выпуклого четырёхугольника авсd , если они пропорциональны чилам 1,2,4,5....
hopesegul hopesegul  19.03.2019 14:10
Впароллилограмме авсд,ад=20см,ав=вд,вк-высота,определите среднюю линию трапеции квсд...
nastyayakushka2 nastyayakushka2  19.03.2019 14:10
Найдите меньшую высоту треугольника со сторонами 15,20 и 25. решение. так как 25 в квадрате=20 в квадрате +15 в квадрате(626=400+225),то по теореме. гипотенуза является...
КилоЛеденцов КилоЛеденцов  28.10.2019 20:14
Стороны основания прямоугольного параллелепипеда относятся как 7: 24 площадь его диагонального сечения равна 50дм^2. найдите его боковую поверхность....
halitovaalsu20 halitovaalsu20  28.10.2019 20:12
Впаралелограмі abcd бісектриса гострого кута перетинає сторону в точці, яка ділить її на відрізку 3 і 8 см, рахуючи від тупого кута. визначити периметр паралелограма...
alinks792 alinks792  28.10.2019 20:09
3. на відрізку ab вибрана точка c, далі на відрізках ас та св як на діаметрахпобудовані кола. пряма bм дотикається першого кола в точці м, а пряма anдотикається другого...
ZevsGromov ZevsGromov  28.10.2019 20:09
Найдите полную поверхность тетраэдра , если площадь одной её грани равна 6см^2....
AnnGo9909 AnnGo9909  28.10.2019 20:07
Радиус одного круга больше чем другой на 2 раза.на сколько процентов она больше? ​...
vadimvadimvadimvadim vadimvadimvadimvadim  28.10.2019 20:07
Сторона ромба равна 5, а одна из его диагоналей равна 6, найти площадь ромба.с объяснением ​...

Популярные вопросы