Втреугольнике abc изображенном на рисунке известно что угол c=90 градусов cdперпендикулярно ab bc=3 см cd=корень из 8 см найдите

Question

Геометрия: Втреугольнике abc изображенном на рисунке известно что угол c=90 градусов cdперпендикулярно ab bc=3 см cd=корень из 8 см найдите длины сторон ac ab bd cos угла b

Evgeniasvavilna · Answer

Из прямоугольного треугольника CDB вычислим BD по теореме Пифагора

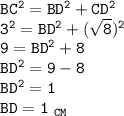
$\tt BC^2=BD^2+CD^2\\ 3^2=BD^2+(\sqrt{8} )^2\\ 9=BD^2+8\\ BD^2=9-8\\ BD^2=1\\ BD=1~ _{CM}$

Высота, опущенная из вершины прямого угла на гипотенузу, равна среднему геометрическому проекций катетов на гипотенузу

$\tt CD^2=AD\cdot BD\\ \\ AD=\dfrac{CD^2}{BD}=\dfrac{(\sqrt{8})^2}{1} =8~_{CM}$

Тогда гипотенуза AB = AD + BD = 8 + 1 = 9 см.

По теореме Пифагора: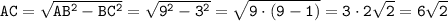 $\tt AC=\sqrt{AB^2-BC^2}=\sqrt{9^2-3^2} =\sqrt{9\cdot(9-1)} =3\cdot2\sqrt{2} =6\sqrt{2}$ см.

Косинус - отношение прилежащего катета к гипотенузе

$\tt \cos\angle B=\dfrac{BC}{AB}=\dfrac{3}{9} =\dfrac{1}{3}$

ответ: AC = 6√2 см; AB = 9 см; BD = 1 см; cos∠B = 1/3.
Втреугольнике abc изображенном на рисунке известно что угол c=90 градусов cdперпендикулярно ab bc=3

Втреугольнике abc изображенном на рисунке известно что угол c=90 градусов cdперпендикулярно ab bc=3 см cd=корень из 8 см найдите длины сторон ac ab bd cos угла b

Популярные вопросы