1. Геометрия
  2. Втреугольнике abc ac=bc

Втреугольнике abc ac=bc , ab=6 cosa= 3\5 найти высоту ch

lui19 lui19    1   10.03.2019 05:50    16

Ответы
NoraDun NoraDun  06.06.2020 23:40

1.cosA=3/5

   cosA=(AB:2)/AC=(6:2)/AC=3/AC

   3/AC=3/5

      AC=5

2.CH-высота треугольника АВС

   Из прямоугольного треугольника АСН находим СН:

   СН=sqrt{AC^2-AH^2}=sqrt{5^2-3^2}=4

ответ: высота треугольника АВС равна 4.

ПОКАЗАТЬ ОТВЕТЫ
DenisPaliy DenisPaliy  06.06.2020 23:40

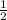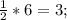
Треугольник ABC - равнобедренный, значит высота СH - медиана => AH=HB=\frac{1}{2}AB=\frac{1}{2}*6=3;
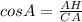
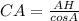
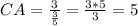
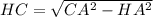
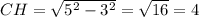
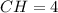Расмотрим треугольник AHC-прямоугольный (угол AHC=90): cosA=\frac{AH}{CA}
CA=\frac{AH}{cosA}
CA=\frac{3}{\frac{3}{5}}=\frac{3*5}{3}=5
По теореме Пифагора: HC=\sqrt{CA^2-HA^2}
CH=\sqrt{5^2-3^2}=\sqrt{16}=4
ответ: CH=4.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
LIONVIP LIONVIP  29.04.2020 13:45
В правильной четырехугольной призме диагональ боковой грани равна 18 см и образует с плоскостью основания угол 30°. Найдите высоту призмы....
KopolbEnufaHtuy KopolbEnufaHtuy  29.04.2020 13:51
Дві сторони трикутника дорівнюють 34 см і 50 см. Висота ділить третю сторону на відрізки, один з яких на 24 см більший за інший. Знайдіть периметр трикутника, його висоту та кути...
nikky228like nikky228like  29.04.2020 13:50
На катете AC прямоугольного треугольника ABC как на диаметре построена окружность, пересекающая гипоте-нузу AB в точке K. Найдите CK, если AC = 2 и ∠A = 20 градусов...
Elluy Elluy  25.12.2020 10:57
1. Определи координаты центра сферы и радиус, если дано уравнение сферы: x2−2⋅x+y2−2⋅y+z2−2⋅z+2=0....
anisinivan09p08i87 anisinivan09p08i87  25.12.2020 10:56
Найдите катет прямоугольного треугольника, если второй катет равен 16,а гопотенуза равно...
моника59 моника59  15.03.2019 01:20
Три точки b. c. d. лежат на одной прямой. известно что bd=17 см,dc=25см. какой может быть длина отрезка bc? подскажите как решить...
FoxLove666 FoxLove666  15.03.2019 01:20
Медиана треугольника делит его периметр пополам.докажите что треугольник равнобедренный...
vorobeowmikhai vorobeowmikhai  15.03.2019 01:20
Сумма вертикальных углов moe и doc, образованных при пересечений прямых mc и de, равна 204 градуса. найдите угол mod. решите...
MegaCrisp1 MegaCrisp1  15.03.2019 01:20
Один из углов равнобедреной трапеции равен 70 градусом найти остальные углы трапеции...
sofiotap3 sofiotap3  15.03.2019 01:20
На рисунке точки a,c,m и p лежат в плоскости альфа,а точка b принадлежит плоскости бета.постройте точку пересечения прямой mp с плоскостью abc.поясните...

Популярные вопросы