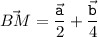Втреугольнике abc,aa1-медиана,m-середина aa1.выразите вектор bm через векторы a=ba и b=bc.
Другие вопросы по теме Геометрия
Популярные вопросы
- Найти лишнее слово: старик, боковой, кормить, рога...
3 - Надо сделать отрицательные предложения...
3 - Вкаком случаи пишется some а в каком any...
2 - Вредный найти противоположное по смыслу слово...
1 - Яв 5 классе мне на казахский язык задали реферат на тему тенге на...
1 - Вкаком предложении следует поставить одну запятую? (знаки препинания...
2 - Лирическое отступление в романе евгений онегин...
2 - Помидорами занято 6/17 огорода,а огурцами-5/17 огорода.какая часть...
2 - Найдите значение выражения: 1) 49 184 + 4 575 : 15 - 62 * 93 - 33...
3 - Морфологический разбор покрытое небо...
1
AB₁║BA₁; A₁B₁║BA.
ABA₁B₁ - параллелограмм т.к. противоположные стороны параллельны.
A₁ - середина BC т.к. AA₁ - медиана, поэтому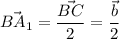
По правилу параллелограмма: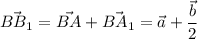
По условию M - середина AA₁. Диагонали в параллелограмме точкой пересечения делятся пополам, поэтому BB₁ ∩ AA₁ = M. Значит,
ответ: